��Ŀ����
������D�ϵĺ���f��x����������㣺������x��D�����ڳ���M��0������|f��x��|��M���������f��x����D�ϵ��н纯��������M��Ϊ����f��x����һ���Ͻ磮��֪����f��x��=
+
��g��x��=log2
������a��0
��1��������f��x��Ϊż��������ʵ��a��ֵ��
��2���ڣ�1���������£�����g��x��������[-1��1]�ϵ������Ͻ繹�ɵļ��ϣ�
��3���ڣ�1���������£��Ƿ���������ĸ�ʵ��k��ʹg��k-cos�ȣ�+g��cos2��-k2����0
��һ�Цȡ�R������������ڣ������kȡֵ�ļ��ϣ��������ڣ�˵�����ɣ�
| ex |
| a |
| a |
| ex |
| 3+ax |
| x+3 |
��1��������f��x��Ϊż��������ʵ��a��ֵ��
��2���ڣ�1���������£�����g��x��������[-1��1]�ϵ������Ͻ繹�ɵļ��ϣ�
��3���ڣ�1���������£��Ƿ���������ĸ�ʵ��k��ʹg��k-cos�ȣ�+g��cos2��-k2����0
��һ�Цȡ�R������������ڣ������kȡֵ�ļ��ϣ��������ڣ�˵�����ɣ�
���㣺�����뷽�̵��ۺ�����
ר�⣺���������ʼ�Ӧ��
��������1��ͨ��f��x��=
+
Ϊż�������Ƴ�a2=1��Ȼ�����a��
��2�����g(x)=log2
��ͨ�����������-1��g��x����1��Ȼ���������g��x��������[-1��1]�ϵ������Ͻ繹�ɼ���Ϊ[1��+�ޣ���
��3�����g��x���Ķ�����Ϊ��-3��3�����ж�f��x�����溯����ͨ��f��x���ǣ�-3��3���ϵļ�������ת��Ϊ��
�Ԧȡ�R�������Ȼ�����k�ķ�Χ��
| ex |
| a |
| a |
| ex |
��2�����g(x)=log2
| 3-x |
| x+3 |
��3�����g��x���Ķ�����Ϊ��-3��3�����ж�f��x�����溯����ͨ��f��x���ǣ�-3��3���ϵļ�������ת��Ϊ��
|
���
������14�֣�
�⣺��1����Ϊf��x��=
+
Ϊż������
����f��-x��=f��x������
+
=
+
��
��(a-
)(ex-
)=0
��a2=1��
��a��0����a=-1����2�֣���
��2���ɣ�1���ã�g(x)=log2
��
��g��x��=log2��-1+
����
��֪g��x��������[-1��1]�ϵ����ݼ���
����-1��g��x����1��
���Ժ���g��x����ֵ��Ϊ[-1��1]��
����|g��x��|��1������5�֣�
�ʺ���g��x��������[-1��1]�ϵ������Ͻ繹�ɼ���Ϊ[1��+�ޣ�������6�֣�
��3����g��x���Ķ�����Ϊ��-3��3��
����f(-x)=lg(
)=-lg(
)=-f(x)��f��x�����溯��������7�֣�
����֪g��x�������䣨-3��3���ϵ����ݼ���
��g��k-cos�ȣ�+g��cos2��-k2����0
��f��k-cos�ȣ���-f��cos2��-k2��=f��k2-cos2�ȣ�����8�֣�
��f��x���ǣ�-3��3���ϵļ�����
��
�Ԧȡ�R�������
��k-cos�ȡ�k2-cos2�ȶԦȡ�R�������
�ã�k-k2��cos��-cos2�ȶԦȡ�R�����������10�֣�
��y=cos��-cos2��=
-(cos��-
)2��
��
��k-k2��-2⇒k��-1��
ͬ������-3��k-cos�ȣ�3�Ԧȡ�R������ã�-2��k��2����12�֣���
��-3��cos2��-k2��3�Ԧȡ�R������ã�-
��k��
����13�֣���
���������ã�-
��k��-1��
���Դ���������k�䷶ΧΪ-
��k��-1����14�֣���
�⣺��1����Ϊf��x��=
| ex |
| a |
| a |
| ex |
����f��-x��=f��x������
| e-x |
| a |
| a |
| e-x |
| ex |
| a |
| a |
| ex |
��(a-
| 1 |
| a |
| 1 |
| ex |
��a2=1��
��a��0����a=-1����2�֣���
��2���ɣ�1���ã�g(x)=log2
| 3-x |
| x+3 |
��g��x��=log2��-1+
| 1 |
| x+3 |
��֪g��x��������[-1��1]�ϵ����ݼ���
����-1��g��x����1��
���Ժ���g��x����ֵ��Ϊ[-1��1]��
����|g��x��|��1������5�֣�
�ʺ���g��x��������[-1��1]�ϵ������Ͻ繹�ɼ���Ϊ[1��+�ޣ�������6�֣�
��3����g��x���Ķ�����Ϊ��-3��3��
����f(-x)=lg(
| 3+x |
| 3-x |
| 3-x |
| 3+x |
����֪g��x�������䣨-3��3���ϵ����ݼ���
��g��k-cos�ȣ�+g��cos2��-k2����0
��f��k-cos�ȣ���-f��cos2��-k2��=f��k2-cos2�ȣ�����8�֣�
��f��x���ǣ�-3��3���ϵļ�����
��
|
��k-cos�ȡ�k2-cos2�ȶԦȡ�R�������
�ã�k-k2��cos��-cos2�ȶԦȡ�R�����������10�֣�
��y=cos��-cos2��=
| 1 |
| 4 |
| 1 |
| 2 |
|
��k-k2��-2⇒k��-1��
ͬ������-3��k-cos�ȣ�3�Ԧȡ�R������ã�-2��k��2����12�֣���
��-3��cos2��-k2��3�Ԧȡ�R������ã�-
| 3 |
| 3 |
���������ã�-
| 3 |
���Դ���������k�䷶ΧΪ-
| 3 |
���������⿼�麯���뷽�̵�Ӧ�ã������ĵ������Լ���ż���Լ������ĺ���������Ӧ�ã�����������������������������������

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
��֪a��b��c��0����a2+
+
+
����СֵΪ��������
| 1 |
| bc |
| 1 |
| a(a-b) |
| 1 |
| b(a-c) |
| A��4 | B��6 | C��8 | D��10 |
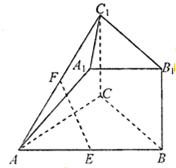 ����ͼ��ʾ�ļ������У��ı���BB1C1C�dz����Σ�BB1��AB��CA=CB��
����ͼ��ʾ�ļ������У��ı���BB1C1C�dz����Σ�BB1��AB��CA=CB��