题目内容
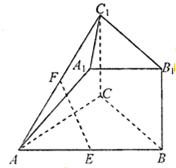 在如图所示的几何体中,四边形BB1C1C是长方形,BB1⊥AB,CA=CB,
在如图所示的几何体中,四边形BB1C1C是长方形,BB1⊥AB,CA=CB,A1B1∥AB,AB=2A1B1,E,F分别是AB,AC1的中点.
(1)求证:EF∥平面BB1C1C;
(2)求证:平面C1AA1⊥平面ABB1A1.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(Ⅰ)连结BC1,可证EF∥BC1,从而证明EF∥平面BB1C1C.
(Ⅱ) 连结A1E,CE,可证C1A1EC是平行四边形,可得A1C1∥EC,即证明B1B⊥EC,可证EC⊥平面ABB1A1,有A1C1⊥平面ABB1A1,即可证明平面C1AA1⊥平面ABB1A1.
(Ⅱ) 连结A1E,CE,可证C1A1EC是平行四边形,可得A1C1∥EC,即证明B1B⊥EC,可证EC⊥平面ABB1A1,有A1C1⊥平面ABB1A1,即可证明平面C1AA1⊥平面ABB1A1.
解答:
解:(Ⅰ)如图,连结BC1.
∵E,F分别是AB,AC1的中点,
∴EF∥BC1.
∵BC1?面BB1C1C,EF?面BB1C1C,
∴EF∥平面BB1C1C.…(4分)
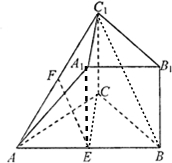
(Ⅱ) 如图,连结A1E,CE.
∵AB∥A1B1,AB=2A1B1,E为中点,
∴BE∥A1B1,且BE=A1B1,即A1B1BE是平行四边形,
∴A1E∥B1B,且A1E=B1B.
由四边形BB1C1C是长方形,知C1C∥B1B,且C1C=B1B,
∴A1E∥C1C,且A1E=C1C,即C1A1EC是平行四边形,
∴A1C1∥EC.…(7分)
∵B1B⊥BC,B1B⊥AB,
∴B1B⊥面ABC,
∴B1B⊥EC. …(9分)
由CA=CB,得EC⊥AB,
∴EC⊥平面ABB1A1.…(10分)
∴A1C1⊥平面ABB1A1.
∵A1C1?平面C1AA1,
∴平面C1AA1⊥平面ABB1A1. …(12分)
∵E,F分别是AB,AC1的中点,
∴EF∥BC1.
∵BC1?面BB1C1C,EF?面BB1C1C,
∴EF∥平面BB1C1C.…(4分)

(Ⅱ) 如图,连结A1E,CE.
∵AB∥A1B1,AB=2A1B1,E为中点,
∴BE∥A1B1,且BE=A1B1,即A1B1BE是平行四边形,
∴A1E∥B1B,且A1E=B1B.
由四边形BB1C1C是长方形,知C1C∥B1B,且C1C=B1B,
∴A1E∥C1C,且A1E=C1C,即C1A1EC是平行四边形,
∴A1C1∥EC.…(7分)
∵B1B⊥BC,B1B⊥AB,
∴B1B⊥面ABC,
∴B1B⊥EC. …(9分)
由CA=CB,得EC⊥AB,
∴EC⊥平面ABB1A1.…(10分)
∴A1C1⊥平面ABB1A1.
∵A1C1?平面C1AA1,
∴平面C1AA1⊥平面ABB1A1. …(12分)
点评:本题主要考察了平面与平面垂直的判定,直线与平面平行的判定,对判定定理的熟练应用是解题的关键,属于中档题.

练习册系列答案
相关题目
命题“?x0∈R,2x0≤0”的否定为( )
| A、?x0∈R,2x0≤0 |
| B、?x0∈R,2x0≥0 |
| C、?x0∈R,2x0<0 |
| D、?x0∈R,2x0>0 |
已知a,b,c满足c<b<a且ac<0,则下列选项中不一定能成立的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知x2+y2-4x-2y-4=0,求
的最大值( )
| 2x+3y+3 |
| x+3 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|