题目内容
直线a，b分别是长方体相邻两个面上的对角线所在直线，则a，b位置关系是 ．
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：a，b对角线开始于同一个顶点时相交；a，b不是开始于同一个顶点时异面；a，b没有平行的可能．
解答：
解：∵直线a，b分别是长方体相邻两个面上的对角线所在直线，
∴a，b可能是相交线，a，b对角线开始于同一个顶点时相交；
a，b也可以是异面，两个对角线a，b不是开始于同一个顶点时异面；
a，b没有平行的可能．
故答案为：相交或异面．
∴a，b可能是相交线，a，b对角线开始于同一个顶点时相交；
a，b也可以是异面，两个对角线a，b不是开始于同一个顶点时异面；
a，b没有平行的可能．
故答案为：相交或异面．
点评：本题考查两条直线的位置关系的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
导学全程练创优训练系列答案
相关题目
给出下列定义：
①对于函数f（x），若存在x0∈R使f（x0）=x0成立，则称x0为函数f（x）的不动点；
②若函数的定义域区间与值域区间完全相同，则称该区间为函数的保值区间．
设函数f（x）=x2-2ax+a2+a（x∈R），则该函数有（ ）
①对于函数f（x），若存在x0∈R使f（x0）=x0成立，则称x0为函数f（x）的不动点；
②若函数的定义域区间与值域区间完全相同，则称该区间为函数的保值区间．
设函数f（x）=x2-2ax+a2+a（x∈R），则该函数有（ ）
| A、一个不动点和一个保值区间 |
| B、两个不动点和一个保值区间 |
| C、两个不动点和两个保值区间 |
| D、两个不动点和三个保值区间 |
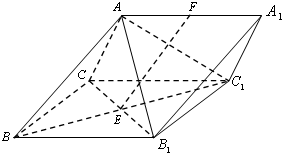如图，三棱柱ABC-A1B1C1中，侧面BB1C1C为菱形，BC1与B1C的交点为E，AC=AB1，F为AA1的中点．已知实数x，y满足
，则x2+y2+4x+6y+14的最大值为（ ）
|
| A、42 | ||
B、
| ||
C、
| ||
| D、46 |
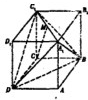如图，在长方体ABCD-A1B1C1D1中，AB=