题目内容
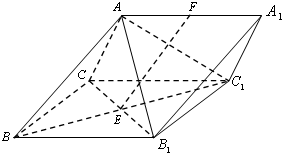 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,BC1与B1C的交点为E,AC=AB1,F为AA1的中点.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,BC1与B1C的交点为E,AC=AB1,F为AA1的中点.(1)求证:面FCB1⊥面ABC1;
(2)求证:EF∥面ABC.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)连接AE,证明B1C⊥平面ABC1,即可证明面FCB1⊥面ABC1;
(2)取BC的中点O,连接OA,OE,证明四边形OEAF是平行四边形,即可证明EF∥面ABC.
(2)取BC的中点O,连接OA,OE,证明四边形OEAF是平行四边形,即可证明EF∥面ABC.
解答:
 证明:(1)连接AE,则
证明:(1)连接AE,则
∵BC1与B1C的交点为E,
∴E为B1C的中点
∵AC=AB1,
∴B1C⊥AE,
∵侧面BB1C1C为菱形,
∴B1C⊥BC1,
∵AE∩BC1=E,
∴B1C⊥平面ABC1,
∵B1C?面FCB1,B1C⊥平面ABC1,
∴面FCB1⊥面ABC1;
(2)取BC的中点O,连接OA,OE,则OE平行且等于
CC1,
∵F为AA1的中点,
∴AF平行且等于
CC1,
∴AF平行且等于OE
∴四边形OEAF是平行四边形,
∴EF∥OA,
∵EF∥OA,EF?面ABC,OA?面ABC,
∴EF∥面ABC.
 证明:(1)连接AE,则
证明:(1)连接AE,则∵BC1与B1C的交点为E,
∴E为B1C的中点
∵AC=AB1,
∴B1C⊥AE,
∵侧面BB1C1C为菱形,
∴B1C⊥BC1,
∵AE∩BC1=E,
∴B1C⊥平面ABC1,
∵B1C?面FCB1,B1C⊥平面ABC1,
∴面FCB1⊥面ABC1;
(2)取BC的中点O,连接OA,OE,则OE平行且等于
| 1 |
| 2 |
∵F为AA1的中点,
∴AF平行且等于
| 1 |
| 2 |
∴AF平行且等于OE
∴四边形OEAF是平行四边形,
∴EF∥OA,
∵EF∥OA,EF?面ABC,OA?面ABC,
∴EF∥面ABC.
点评:本题考查平面与平面垂直的证明,考查直线与平面平行的判定,考查学生分析解决问题的能力,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
正方体ABCD-A1B1C1D1中,E,F分别是棱AD,AA1的中点,则D1E和B1F所成的角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若使得方程
-x-m=0有实数解,则实数m的取值范围为( )
| 16-x2 |
A、-4
| ||||
B、-4≤m≤4
| ||||
| C、-4≤m≤4 | ||||
D、4≤m≤4
|
 正四棱锥S-ABCD中,底面正方形ABCD的边长为a,侧棱长为2a,M为SA中点,N为棱SC中点,求异面直线DM与BN所成角的余弦值.
正四棱锥S-ABCD中,底面正方形ABCD的边长为a,侧棱长为2a,M为SA中点,N为棱SC中点,求异面直线DM与BN所成角的余弦值.