题目内容
已知椭圆C的离心率e=
,长轴的左右端点分别为A1(-
,0),A2(
,0)
(Ⅰ)求椭圆C的方程;
(Ⅱ)设动直线l:y=kx+b与曲线C有且只有一个公共点P,且与直线x=2相交于点Q.求证:以PQ为直径的圆过定点N(1,0).
| ||
| 2 |
| 2 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设动直线l:y=kx+b与曲线C有且只有一个公共点P,且与直线x=2相交于点Q.求证:以PQ为直径的圆过定点N(1,0).
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据离心率e=
,长轴的左右端点分别为A1(-
,0),A2(
,0),求出几何量,即可求椭圆C的方程;
(Ⅱ)直线l:y=kx+b与曲线C联立,消去y,利用曲线C与直线l只有一个公共点,得△=0,可得b2=2k2+1,求出P,Q的坐标,证明
•
=1+
-
-1=0,可得以PQ为直径的圆恒过定点.
| ||
| 2 |
| 2 |
| 2 |
(Ⅱ)直线l:y=kx+b与曲线C联立,消去y,利用曲线C与直线l只有一个公共点,得△=0,可得b2=2k2+1,求出P,Q的坐标,证明
| PN |
| QN |
| 2k |
| b |
| 2k |
| b |
解答:
解:(Ⅰ)由已知a=
,e=
=
,
∴c=1,b=
=1,
∴椭圆C的方程为
+y2=1;
(Ⅱ)
消去得(2k2+1)x2+4kbx+2b2-2=0,
∵曲线C与直线l只有一个公共点,∴△=0,
可得b2=2k2+1(*),
设P(xP,yP),
∴xP=
=-
,yP=kxP+b=
,∴P(-
,
).
又由
,∴Q(2,2k+b),
∵N(1,0),∴
=(1+
,-
),
=(1,2k+b)
∴
•
=1+
-
-1=0,∴PN⊥QN,
∴以PQ为直径的圆过定点N(1,0).
| 2 |
| c |
| a |
| ||
| 2 |
∴c=1,b=
| a2-c2 |
∴椭圆C的方程为
| x2 |
| 2 |
(Ⅱ)
|
∵曲线C与直线l只有一个公共点,∴△=0,
可得b2=2k2+1(*),
设P(xP,yP),
∴xP=
| -4kb |
| 2(2k2+1) |
| 2k |
| b |
| 1 |
| b |
| 2k |
| b |
| 1 |
| b |
又由
|
∵N(1,0),∴
| PN |
| 2k |
| b |
| 1 |
| b |
| NQ |
∴
| PN |
| QN |
| 2k |
| b |
| 2k |
| b |
∴以PQ为直径的圆过定点N(1,0).
点评:本题主要考查椭圆方程、圆的性质、直线与圆锥曲线的位置关系,考查运算能力,考查化归思想,属于中档题.

练习册系列答案
相关题目
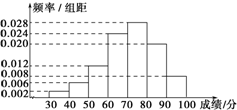 某中学为了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是
某中学为了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是