题目内容
设等差数列{an}的前n项和为Sn,且S1=1,S3=6,则
的最大值为 .
| n |
| Sn+8 |
考点:等差数列的性质
专题:等差数列与等比数列
分析:设等差数列{an}的首项为a1,公差为d,由S1=1,S3=6联立方程组求出a1,d,进一步求出等差数列{an}的前n项和为Sn,代入
后整理,最后利用基本不等式求最值.
| n |
| Sn+8 |
解答:
解:设等差数列{an}的首项为a1,公差为d,
由S1=1,S3=6,得:
,解得:
.
∴Sn=na1+
=n+
=
.
∴
=
=
=
≤
=
.
当且仅当n=
,即n=4时上式取等号.
故答案为:
.
由S1=1,S3=6,得:
|
|
∴Sn=na1+
| n(n-1)d |
| 2 |
| n2-n |
| 2 |
| n(n+1) |
| 2 |
∴
| n |
| Sn+8 |
| n | ||
|
| 2n |
| n2+n+16 |
| 2 | ||
n+
|
| 2 | ||||
2
|
| 2 |
| 9 |
当且仅当n=
| 16 |
| n |
故答案为:
| 2 |
| 9 |
点评:本题考查了等差数列的性质,考查了等差数列的前n项和公式,训练了利用基本不等式求最值,是中低档题.

练习册系列答案
相关题目
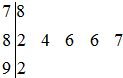 如图是2010年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为( )
如图是2010年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为( )| A、4.84 | B、0.8 |
| C、1.6 | D、3.2 |
若复数z满足(z+2)i=5+5i(i为虚数单位),则z为( )
| A、3+5i | B、3-5i |
| C、-3+5i | D、-3-5i |

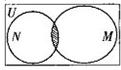 已知全集U=R,集合M={x|-2≤x-1≤2}和N={x|x=2k-1,k=1,2,…}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合的元素共有
已知全集U=R,集合M={x|-2≤x-1≤2}和N={x|x=2k-1,k=1,2,…}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合的元素共有