题目内容
已知{an}是各项均为正数的等比数列,且a1=1,3a1是 a3,a5的等差中项.
(1)求{an}的通项公式;
(2)设bn=log2an,求数列{
}的前n项和Tn.
(1)求{an}的通项公式;
(2)设bn=log2an,求数列{
| 1 |
| bnbn+1 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由题意可得a3+a5=6a1,解得q,即可得出结论;
(2)利用裂项法求和,由(1)得bn=log2an=
,
=
(n≥2).
=
=4(
-
),即可求得结论.
(2)利用裂项法求和,由(1)得bn=log2an=
| n-1 |
| 2 |
| 1 |
| bn |
| 2 |
| n-1 |
| 1 |
| bnbn+1 |
| 4 |
| (n-1)n |
| 1 |
| n-1 |
| 1 |
| n |
解答:
解:(1)∵a1=1,3a1是 a3,a5的等差中项.
∴a3+a5=6a1,
即q2+q4=6,解得q2=2,q=
,
∴an=1•(
)n-1=2
.
(2)由(1)得bn=log2an=
,
=
(n≥2).
∴
=
=4(
-
),
∴Tn=4(1-
+
-
+…+
-
)=4(1-
)=
.
∴a3+a5=6a1,
即q2+q4=6,解得q2=2,q=
| 2 |
∴an=1•(
| 2 |
| n-1 |
| 2 |
(2)由(1)得bn=log2an=
| n-1 |
| 2 |
| 1 |
| bn |
| 2 |
| n-1 |
∴
| 1 |
| bnbn+1 |
| 4 |
| (n-1)n |
| 1 |
| n-1 |
| 1 |
| n |
∴Tn=4(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n |
| 4(n-1) |
| n |
点评:本题主要考查等差数列的性质及裂项法求数列的和等知识,考查学生的运算求解能力,属于中档题.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
下列函数中为奇函数的是( )
| A、f(x)=x3 |
| B、f(x)=x2+1 |
| C、f(x)=cosx |
| D、f(x)=lgx |
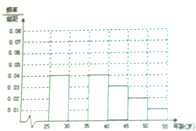 某班同学利用五一劳动节进行社会实践,对信宜城区[25,55]岁的人群随机抽取n人进行生活习惯是否符合低碳观念的调查.得到如图所示的人数频率分布直方图,若生活习惯符合低碳观念,则称为“低碳族”,否则称为“非低碳族”,得到如图所示的人数统计表.
某班同学利用五一劳动节进行社会实践,对信宜城区[25,55]岁的人群随机抽取n人进行生活习惯是否符合低碳观念的调查.得到如图所示的人数频率分布直方图,若生活习惯符合低碳观念,则称为“低碳族”,否则称为“非低碳族”,得到如图所示的人数统计表.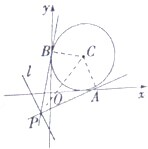 已知P是直线l:3x+4y+8=0上的动点,PA,PB是圆C:x2+y2-2x-2y+1=0的两条切线,A、B是切点.
已知P是直线l:3x+4y+8=0上的动点,PA,PB是圆C:x2+y2-2x-2y+1=0的两条切线,A、B是切点.