题目内容
正三棱锥P-ABC的底面边长为1,E,F,G,H分别是PA,AC,BC,PB的中点,四边形EFGH的面积为S,则S的取值范围是 .
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:由已知中正三棱锥P-ABC的底面边长为1,E,F,G,H,分别是PA,AC,BC,PD的中点,我们可判断出四边形EFGH为一个矩形,一边长为
,另一边长大于底面的外接圆的半径的一半,进而得到答案.
| 1 |
| 2 |
解答:
 解:∵棱锥P-ABC为底面边长为1的正三棱锥
解:∵棱锥P-ABC为底面边长为1的正三棱锥
∴AB⊥PC
又∵E,F,G,H,分别是PA,AC,BC,PD的中点,
∴EH=FG=
AB=
,EF=HG=
PC
则四边形EFGH为一个矩形
又∵PC>
,
∴EF>
,
,
∴四边形EFGH的面积S的取值范围是(
,+∞),
故答案为:(
,+∞)
 解:∵棱锥P-ABC为底面边长为1的正三棱锥
解:∵棱锥P-ABC为底面边长为1的正三棱锥∴AB⊥PC
又∵E,F,G,H,分别是PA,AC,BC,PD的中点,
∴EH=FG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则四边形EFGH为一个矩形
又∵PC>
| ||
| 3 |
∴EF>
| ||
| 6 |
| ||
| 12 |
∴四边形EFGH的面积S的取值范围是(
| ||
| 12 |
故答案为:(
| ||
| 12 |
点评:本题考查的知识点是棱锥的结构特征,其中根据正三棱锥的结构特征,判断出AB⊥PC这,进而得到四边形EFGH为一个矩形是解答本题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
复数z=1+i,则
=( )
| 1+z |
| 1-z |
| A、2-i | B、2+i |
| C、-1+2i | D、1+2i |
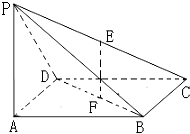 如图在四棱锥P-ABCD中,底面abcd是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
如图在四棱锥P-ABCD中,底面abcd是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=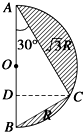 如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,∠BAC=30°,则此几何体的体积为
如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,∠BAC=30°,则此几何体的体积为