题目内容
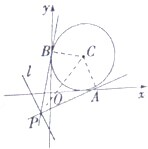 已知P是直线l:3x+4y+8=0上的动点,PA,PB是圆C:x2+y2-2x-2y+1=0的两条切线,A、B是切点.
已知P是直线l:3x+4y+8=0上的动点,PA,PB是圆C:x2+y2-2x-2y+1=0的两条切线,A、B是切点.(1)求四边形PACB面积的最小值;
(2)直线l上是否存在点P,使∠BPA=60°?若存在,求出点P的坐标,若不存在,说明理由.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)由圆C的标准方程可得圆心为(1,1),半径为1,由于四边形PACB面积等于2×
PA×AC=PA,而PA=
,故当PC最小时,四边形PACB面积最小,又PC的最小值等于圆心C到直线l的距离d,求出d 即可得到四边形PACB面积的最小值;
(2)假设存在一点使∠BPA=60°,此时∠CPA=30,根据直角三角形性质可知,圆心到直线上P(x,y)点距离为半径2倍,也就是2,可见它小于圆心到直线的最短距离3,可得结论.
| 1 |
| 2 |
| PC2-1 |
(2)假设存在一点使∠BPA=60°,此时∠CPA=30,根据直角三角形性质可知,圆心到直线上P(x,y)点距离为半径2倍,也就是2,可见它小于圆心到直线的最短距离3,可得结论.
解答:
解:圆C:x2+y2-2x-2y+1=0,即(x-1)2+(y-1)2=1,表示以C(1,1)为圆心,以1为半径的圆.
由于四边形PACB面积等于2×
PA×AC=PA,而PA=
,
故当PC最小时,四边形PACB面积最小.
又PC的最小值等于圆心C到直线l:3x+4y+8=0 的距离d,而d=
=3,
故四边形PACB面积的最小的最小值为
=2
;
(2)假设存在一点使∠BPA=60°,此时∠CPA=30,根据直角三角形性质可知,圆心到直线上P(x,y)点距离为半径2倍,也就是2,可见它小于圆心到直线的最短距离3,因此该点不存在.
由于四边形PACB面积等于2×
| 1 |
| 2 |
| PC2-1 |
故当PC最小时,四边形PACB面积最小.
又PC的最小值等于圆心C到直线l:3x+4y+8=0 的距离d,而d=
| |3++8| | ||
|
故四边形PACB面积的最小的最小值为
| 9-1 |
| 2 |
(2)假设存在一点使∠BPA=60°,此时∠CPA=30,根据直角三角形性质可知,圆心到直线上P(x,y)点距离为半径2倍,也就是2,可见它小于圆心到直线的最短距离3,因此该点不存在.
点评:本题考查直线和圆的位置关系,点到直线的距离公式,判断故当PC最小时,四边形PACB面积最小,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
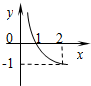 已知函数f(x)=logax(a>0,且a≠1)的图象如图所示,函数y=g(x)是函数y=f(x)的反函数,则函数y=g(x)的解析式为( )
已知函数f(x)=logax(a>0,且a≠1)的图象如图所示,函数y=g(x)是函数y=f(x)的反函数,则函数y=g(x)的解析式为( )| A、g(x)=2x | ||
B、g(x)=(
| ||
C、g(x)=log
| ||
| D、g(x)=log2x |
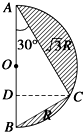 如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,∠BAC=30°,则此几何体的体积为
如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,∠BAC=30°,则此几何体的体积为