题目内容
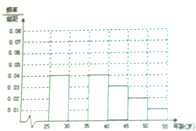 某班同学利用五一劳动节进行社会实践,对信宜城区[25,55]岁的人群随机抽取n人进行生活习惯是否符合低碳观念的调查.得到如图所示的人数频率分布直方图,若生活习惯符合低碳观念,则称为“低碳族”,否则称为“非低碳族”,得到如图所示的人数统计表.
某班同学利用五一劳动节进行社会实践,对信宜城区[25,55]岁的人群随机抽取n人进行生活习惯是否符合低碳观念的调查.得到如图所示的人数频率分布直方图,若生活习惯符合低碳观念,则称为“低碳族”,否则称为“非低碳族”,得到如图所示的人数统计表.(1)请补全频率分布直方图,并估计样本的众数和中位数;
(2)并求n、a、p的值;
(3)从[35,50)岁年龄段三个小组的“低碳族”中采用分层抽样法抽取38人参加户外低碳体验活动,各小组应该抽取的人数为多少?
| 组数 | 分组 | 低碳族的人数 | 占本组的频率 |
| 第一组 | [25,30﹚ | 120 | 0.6 |
| 第二组 | [30,35﹚ | 195 | p |
| 第三组 | [35,40﹚ | 100 | 0.5 |
| 第四组 | [40,45﹚ | a | 0.4 |
| 第五组 | [45,50﹚ | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
考点:频率分布直方图,分层抽样方法
专题:概率与统计
分析:(1)根据频率分布直方图,求出第二组的频率,补全频率分布直方图;求出样本的众数和中位数;
(2)根据频率分布直方图,求出各小组抽取的人数,计算样本容量n及p、a的值;
(3)求出[35,50)岁年龄段三个小组的“低碳族”人数是多少,再利用分层抽样法求出各小组应该抽取的人数是多少.
(2)根据频率分布直方图,求出各小组抽取的人数,计算样本容量n及p、a的值;
(3)求出[35,50)岁年龄段三个小组的“低碳族”人数是多少,再利用分层抽样法求出各小组应该抽取的人数是多少.
解答:
解:(1)∵0.04×5+0.04×5+0.03×5+0.02×5+0.01×5=0.7,
∴第二组的频率是1-0.7=0.3,
∴补全频率分布直方图,如图所示;
∴样本的众数是
=32.5,
∵0.04×5+0.06×5=0.5,
∴中位数是35;
(2)根据频率分布直方图,得;
[25,30)内抽取的人数是
=200,
[30,35)内抽取的人数是200×
=300
[35,40)内抽取的人数是
=200,
[40,45)内抽取的人数是50×3=150,
[45,50)内抽取的人数是
=100,
[50,55]内抽取的人数是
=50;
∴样本容量n=200+300+200+150+100+50=1000;
p=
=0.65、a=150×0.4=60;
(3)[35,50)岁年龄段三个小组的“低碳族”人数是100、60、30,
从中采用分层抽样法抽取38人参加户外低碳体验活动,各小组应该抽取的人数分别为
38×
=20,
38×
=12,
38×
=6.
∴第二组的频率是1-0.7=0.3,
∴补全频率分布直方图,如图所示;

∴样本的众数是
| 30+35 |
| 2 |
∵0.04×5+0.06×5=0.5,
∴中位数是35;
(2)根据频率分布直方图,得;
[25,30)内抽取的人数是
| 120 |
| 0.6 |
[30,35)内抽取的人数是200×
| 0.06 |
| 0.04 |
[35,40)内抽取的人数是
| 100 |
| 0.5 |
[40,45)内抽取的人数是50×3=150,
[45,50)内抽取的人数是
| 30 |
| 0.3 |
[50,55]内抽取的人数是
| 15 |
| 0.3 |
∴样本容量n=200+300+200+150+100+50=1000;
p=
| 195 |
| 300 |
(3)[35,50)岁年龄段三个小组的“低碳族”人数是100、60、30,
从中采用分层抽样法抽取38人参加户外低碳体验活动,各小组应该抽取的人数分别为
38×
| 100 |
| 100+60+30 |
38×
| 60 |
| 100+60+30 |
38×
| 30 |
| 100+60+30 |
点评:本题考查了频率分布直方图的应用问题,也考查了分层抽样方法的应用问题,是综合性题目.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
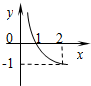 已知函数f(x)=logax(a>0,且a≠1)的图象如图所示,函数y=g(x)是函数y=f(x)的反函数,则函数y=g(x)的解析式为( )
已知函数f(x)=logax(a>0,且a≠1)的图象如图所示,函数y=g(x)是函数y=f(x)的反函数,则函数y=g(x)的解析式为( )| A、g(x)=2x | ||
B、g(x)=(
| ||
C、g(x)=log
| ||
| D、g(x)=log2x |
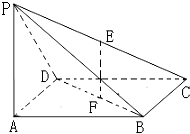 如图在四棱锥P-ABCD中,底面abcd是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
如图在四棱锥P-ABCD中,底面abcd是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=