题目内容
已知复数z=
+（a2-5a-6）i（a∈R）．
（1）求实数a为何值时，z为实数；
（2）求实数a为何值时，z为虚数；
（3）求实数a为何值时，z为纯虚数．
| a2-7a+6 |
| a+1 |
（1）求实数a为何值时，z为实数；
（2）求实数a为何值时，z为虚数；
（3）求实数a为何值时，z为纯虚数．
考点：复数的基本概念
专题：数系的扩充和复数
分析：首先求出实部和虚部等于0的a值，然后由复数是实数、虚数和纯虚数的条件得到a的值．
解答：
解：由
=0，解得：a=1或a=6．
由a2-5a-6=0，解得：a=-1或a=6．
（1）当实数a=6时，z为实数；
（2）当实数a≠-1且a≠6时，z为虚数；
（3）当实数a=1时，z为纯虚数．
| a2-7a+6 |
| a+1 |
由a2-5a-6=0，解得：a=-1或a=6．
（1）当实数a=6时，z为实数；
（2）当实数a≠-1且a≠6时，z为虚数；
（3）当实数a=1时，z为纯虚数．
点评：本题考查了复数的基本概念，考查了不等式的解法，是基础题．
练习册系列答案
相关题目
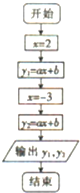如图是为解决某个问题而绘制的程序框图，仔细分析各图框内的内容及框图之间的关系，回答下面的问题：
如图1，在Rt△ABC中，∠C=90°，BC=3，AC=6，D，E分别是Ac，AB上的点，且DE∥BC，DE=2，将△ADE沿DE折起到A1DE的位置，使A1C⊥CD，如图2．
如图，在三棱柱ABC-A1B1C1中，AA1⊥平面A1B1C1，A1B1⊥A1C1，B1C⊥AC1，AB=2，AC=1则该三棱柱的体积为