题目内容
已知函数f(x)=x2-2lnx.
(1)求函数f(x)的单调区间;
(2)对于函数图象上的不同两点A(x1,y1),B(x2,y2),如果在函数图象上存在点P(x0,y0)(其中x0在x1与x2之间),使得点P处的切线l平行于直线AB,则称AB存在“伴随切线”,当x0=
时,又称AB存在“中值伴随切线”.试判断函数f(x)的图象上是否存在“中值伴随切线”,若存在,请求出“中值伴随切线”.
(1)求函数f(x)的单调区间;
(2)对于函数图象上的不同两点A(x1,y1),B(x2,y2),如果在函数图象上存在点P(x0,y0)(其中x0在x1与x2之间),使得点P处的切线l平行于直线AB,则称AB存在“伴随切线”,当x0=
| x1+x2 |
| 2 |
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)求出函数的定义域,函数的导数,通过f′(x)=
大于、小于0,即可求出函数的单调区间.
(2)假设存在不同两点A(x1,y1),B(x2,y2)(不妨设0<x1<x2),使得AB存在“中值伴随切线”,则
=f′(
),化简后,构造函数g(x)=lnx-
,通过函数的导数,利用定义,推出结论矛盾,得到结果.
| 2(x+1)(x-1) |
| x |
(2)假设存在不同两点A(x1,y1),B(x2,y2)(不妨设0<x1<x2),使得AB存在“中值伴随切线”,则
| f(x1)-f(x2) |
| x1-x2 |
| x1+x2 |
| 2 |
| 2x-2 |
| x+1 |
解答:
解:(1)函数f(x)=x2-2lnx.函数的定义域为:x>0,
∴f′(x)=
,
由f′(x)>0知:递增区间为(1,+∞),
由f′(x)<0知,递减区间为(0,1].3分
(2)假设存在不同两点A(x1,y1),B(x2,y2)(不妨设0<x1<x2),使得AB存在“中值伴随切线”,则
=f′(
),
化简得:
=
,即
=ln
.
设函数g(x)=ln x-
,则g′(x)=
-
=
,
当x∈(0,1)时,g′(x)>0,即g(x)在(0,1]上是增函数.
又0<
<1,所以g(
)<g(1)=0,即
>ln
,与上面结论矛盾,
所以在函数f(x)的图象上是不存在不同两点A,B,使得AB存在“中值伴随切线”.12分.
∴f′(x)=
| 2(x+1)(x-1) |
| x |
由f′(x)>0知:递增区间为(1,+∞),
由f′(x)<0知,递减区间为(0,1].3分
(2)假设存在不同两点A(x1,y1),B(x2,y2)(不妨设0<x1<x2),使得AB存在“中值伴随切线”,则
| f(x1)-f(x2) |
| x1-x2 |
| x1+x2 |
| 2 |
化简得:
| 2 |
| x1+x2 |
| lnx1-lnx2 |
| x1-x2 |
2•
| ||
|
| x1 |
| x2 |
设函数g(x)=ln x-
| 2x-2 |
| x+1 |
| 1 |
| x |
| 4 |
| (x+1)2 |
| (x-1)2 |
| x(x+1)2 |
当x∈(0,1)时,g′(x)>0,即g(x)在(0,1]上是增函数.
又0<
| x1 |
| x2 |
| x1 |
| x2 |
2•
| ||
|
| x1 |
| x2 |
所以在函数f(x)的图象上是不存在不同两点A,B,使得AB存在“中值伴随切线”.12分.
点评:本题考查函数的导数的综合应用,切线方程的求法,新定义以及构造法的应用,考查分析问题解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知全集U={1,2,3,4,5,6,7,8,9,10},集合A={1,3,5,7},B={2,4,5,7},则∁UA∩∁UB=( )
| A、{6,8,9,10} |
| B、{1,2,3,6,8,9,10} |
| C、{5,7} |
| D、{1,2,3,4,5,7} |
命题“?x>1,log2x>0”的否定形式是( )
| A、?x0>1,log2x≤0 |
| B、?x0≤1,log2x≤0 |
| C、?x>1,log2x≤0 |
| D、?x≤1,log2x>0 |
在△ABC中,过中线AD的中点E任作一条直线分别交AB,AC于M,N两点,若
=x
,
=y
,则4x+y的最小值为( )
| AM |
| AB |
| AN |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
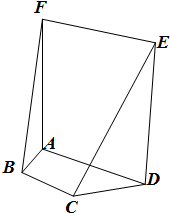 如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=2
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=2