题目内容
若曲线C1:ρ=2cosθ与曲线C2:y-mx-m=0有2个不同的交点,则实数m的取值范围是( )
A、(-
| ||||||||
B、(-
| ||||||||
C、[-
| ||||||||
D、(-∞,-
|
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把极坐标化为直角坐标方程,直线与圆的位置关系转化为圆心到直线的距离与半径的关系,即可得出.
解答:
解:曲线C1:ρ=2cosθ化为ρ2=2ρcosθ,∴x2+y2=2x,即曲线C1:(x-1)2+y2=1,图象为圆心为(1,0),半径为1的圆;
曲线C2:y-mx-m=0,直线y-mx-m=0恒过定点(-1,0),即曲线C2图象为恒过定点(-1,0)的直线l.
当圆心(1,0)到直线l:y-mx-m=0的距离小于1时,它们有2个不同的交点,
∴
<1,解得:m∈(-
,
),
故选:A.
曲线C2:y-mx-m=0,直线y-mx-m=0恒过定点(-1,0),即曲线C2图象为恒过定点(-1,0)的直线l.
当圆心(1,0)到直线l:y-mx-m=0的距离小于1时,它们有2个不同的交点,
∴
| |-m-m| | ||
|
| ||
| 3 |
| ||
| 3 |
故选:A.
点评:本题考查了把极坐标化为直角坐标方程、直线与圆的位置关系转化为圆心到直线的距离与半径的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
已知双曲线的渐近线方程是y=±
x,焦点在x轴上,焦距为20,则它的方程为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
古代“五行”学认为:“物质分金、木、土、水、火五种属性,金克木,木克土,土克水,水克火,火克金.”将五种不同属性的物质任意排成一列,但排列中属性相克的两种物质不相邻,则这样的排列方法有多少种(结果用数字表示).( )
| A、5 | B、10 | C、20 | D、120 |
为了得到y=sin2x的图象,只需将y=sin(2x+
)的图象( )
| π |
| 3 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
在直三棱柱ABC-A1B1C1中,若
=
,
=
,
=
,则
等于( )
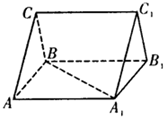
| CA |
| a |
| CB |
| b |
| CC1 |
| c |
| A1B |

A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
若f(x)=
,f(f(1))=1,则a的值为.
|
| A、1 | B、2 | C、-1 | D、-2 |
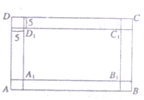 某市政府为了打造宜居城市,计划在公园内新建一个如图所示的矩形ABCD的休闲区,内不是矩形景观区A1B1C1D1,景观区四周是人行道,已知景观区的面积为8000平方米,人行道的宽为5米(如图所示).
某市政府为了打造宜居城市,计划在公园内新建一个如图所示的矩形ABCD的休闲区,内不是矩形景观区A1B1C1D1,景观区四周是人行道,已知景观区的面积为8000平方米,人行道的宽为5米(如图所示).