题目内容
定义函数f(x)如下:对于实数x,如果存在整数m,使得|x-m|<
,则f(x)=m.已知等比数列{an}的首项a1=1,公比为q<0,又f(a1)+f(a2)+f(a3)=3,则q的取值范围是 .
| 1 |
| 2 |
考点:等比数列的通项公式
专题:等差数列与等比数列
分析:利用新定义函数f(x),对q分类讨论即可得出.
解答:
解:∵等比数列{an}的首项a1=1,公比为q<0,
∴an=qn-1.
①假设-
<q<0,
∵a1=1,∴由|1-m|<
,可得m=1.
∴f(a1)=1.
∵a2=q,∴由|q-m|<
,可得m=-1,∴f(a2)=-1,
同理由a3=q2,可得f(a3)=0,
不满足f(a1)+f(a2)+f(a3)=3,舍去.
②当q=-
时,f(a1)=1,|-
-m|<
,m无整数解,舍去.
③当-1<q<-
时,f(a1)=1,
由|q-m|<
,可得m=-1,∴f(a2)=-1.
由|q2-m|<
,可得m≠3,不满足f(a1)+f(a2)+f(a3)=3,舍去.
④当q=-1时,f(a1)=1,|-1-m|<
,m=-1,可得f(a2)=-1.
由|q2-m|<
,可得m=1,不满足f(a1)+f(a2)+f(a3)=3,舍去.
⑤当-
<q<-1时,f(a1)=1,由|q-m|<
,可得m=-1,∴f(a2)=-1.
∵满足f(a1)+f(a2)+f(a3)=3,∴m=3.
不满足|q2-3|<
,舍去.
⑥当q=-
时,f(a1)=1,由|-
-m|<
,m无整数解,舍去.
⑦当-2<q<-
时,f(a1)=1,由|q-m|<
,可得m=-2,∴f(a2)=-2.
∵满足f(a1)+f(a2)+f(a3)=3,
∴m=4.
由|q2-4|<
,可得
<q2<
,而
<q2<4,
∴
<q2<4,解得-2<q<-
.
⑧当m≤-2时,都不满足条件.
综上可得:q的取值范围是(-2,-
).
故答案为:(-2,-
).
∴an=qn-1.
①假设-
| 1 |
| 2 |
∵a1=1,∴由|1-m|<
| 1 |
| 2 |
∴f(a1)=1.
∵a2=q,∴由|q-m|<
| 1 |
| 2 |
同理由a3=q2,可得f(a3)=0,
不满足f(a1)+f(a2)+f(a3)=3,舍去.
②当q=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
③当-1<q<-
| 1 |
| 2 |
由|q-m|<
| 1 |
| 2 |
由|q2-m|<
| 1 |
| 2 |
④当q=-1时,f(a1)=1,|-1-m|<
| 1 |
| 2 |
由|q2-m|<
| 1 |
| 2 |
⑤当-
| 3 |
| 2 |
| 1 |
| 2 |
∵满足f(a1)+f(a2)+f(a3)=3,∴m=3.
不满足|q2-3|<
| 1 |
| 2 |
⑥当q=-
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
⑦当-2<q<-
| 3 |
| 2 |
| 1 |
| 2 |
∵满足f(a1)+f(a2)+f(a3)=3,
∴m=4.
由|q2-4|<
| 1 |
| 2 |
| 7 |
| 2 |
| 9 |
| 2 |
| 9 |
| 4 |
∴
| 7 |
| 2 |
| ||
| 2 |
⑧当m≤-2时,都不满足条件.
综上可得:q的取值范围是(-2,-
| ||
| 2 |
故答案为:(-2,-
| ||
| 2 |
点评:本题考查了新定义函数、分类讨论思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知集合M={x|-2<x<2},N={x|-1<x<3},则M∩N=( )
| A、{x|x<-2} |
| B、{x|x>3} |
| C、{x|-1<x<2} |
| D、{x|2<x<3} |
在△ABC中,若
•(
-2
)=0,则△ABC的形状为 ( )
| AB |
| AB |
| AC |
| A、直角三角形 |
| B、等腰三角形 |
| C、等边三角形 |
| D、等腰直角三角形 |
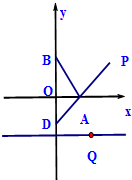 如图,在平面直角坐标系中,O为坐标原点,点B(0,1),且点A(a,0)(a≠0)是x轴上动点,过点A作线段AB的垂线交y轴于点D,在直线AD上取点P,使AP=DA.
如图,在平面直角坐标系中,O为坐标原点,点B(0,1),且点A(a,0)(a≠0)是x轴上动点,过点A作线段AB的垂线交y轴于点D,在直线AD上取点P,使AP=DA.