Question

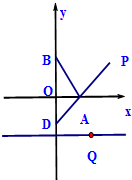如图，在平面直角坐标系中，O为坐标原点，点B（0，1），且点A（a，0）（a≠0）是x轴上动点，过点A作线段AB的垂线交y轴于点D，在直线AD上取点P，使AP=DA．
（Ⅰ）求动点P的轨迹C的方程；
（Ⅱ）点Q是直线y=-1上的一个动点，过点Q作轨迹C的两条切线切点分别为M，N求证：QM⊥QN．

Answer 1

考点：轨迹方程,直线与圆锥曲线的关系

专题：圆锥曲线的定义、性质与方程

分析：（1）由已知可得AP⊥AB，得到直线AP的斜率，写出直线方程，利用AP=AD，求出x，y满足的关系；
（2）由（1）可知，直线MQ，NQ都是抛物线的切线，得到它们的斜率（用各自的坐标表示，）利用两点式得到的直线斜率与求导得到斜率相等，得到x₁，x₂是方程x²-2tx-4=0的两个根，利用根与系数的关系结合向量垂直的性质得到关于Q的坐标的代数式值为0．

解答： 解：（1）设动点P（x，y），k_AB=-

1

a

，∵AP⊥AB，∴k_AP=a，∴直线AP的方程为y=a（x-a）．…（2分）
由AP=DA，即A为线段PD的中点，∴x=2a，y=a²，
∴点P的轨迹C的方程是x²=4y（y≠0）．…（5分）
（2）设Q（t，-1），M（x₁，

x12

4

），N（x₂，

x22

4

），∵x²=4y，
∴y′=

1

2

x． 
∴k_MQ=

1

2

x₁，k_NQ=

1

2

x₂，
∴

x12 4 +1

x1-t

=

1

2

x1整理得x₁²-2tx₁-4=0．…（8分）
同理x₂²-2tx₂-4=0，
∴x₁，x₂是方程x²-2tx-4=0的两个根，
x₁+x₂=2t，x₁x₂=-4．…（9分）
∴

QM

•

QN

=（x₁-t，

x12

4

+1）（x₂-t，

x22

4

+1）=x₁x₂-t（x₁+x₂）+t²+

1

16

x12x22+

1

4

(x12+x22)+1 
=-4-2t²+t²+1+

1

4

（4t²+8）+1=0，
∴QM⊥QN．…（14分）

点评：本题考查了轨迹方程的求法以及利用向量解决几何中线段垂直问题，运算量较大，注意细心解答，属于中档题．