题目内容
已知函数f（x）=
，则f（
）+f（
）+f（
）+…+f（
）= ．
| 3x-2 |
| 2x-1 |
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 2014 |
| 2015 |
考点：函数的值
专题：函数的性质及应用
分析：由f（x）+f（1-x）=
+
=3，能求出f（
）+f（
）+f（
）+…+f（
）的值．
| 3x-2 |
| 2x-1 |
| 3(1-x)-2 |
| 2(1-x)-1 |
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 2014 |
| 2015 |
解答：
解：∵f（x）=
，
∴f（x）+f（1-x）=
+
=3，
∴f（
）+f（
）+f（
）+…+f（
）
=1007×3
=3021．
故答案为：3021．
| 3x-2 |
| 2x-1 |
∴f（x）+f（1-x）=
| 3x-2 |
| 2x-1 |
| 3(1-x)-2 |
| 2(1-x)-1 |
∴f（
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 2014 |
| 2015 |
=1007×3
=3021．
故答案为：3021．
点评：本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
全能测控期末小状元系列答案
相关题目
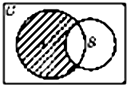已知全集U=R，集合A={y|y=ln（x2+1），x∈R}，集合A={x||x-2|≤1}，则如图所示的阴影部分表示的集合为（ ）| A、{x|0≤x＜1或x＞3} |
| B、{x|0≤x＜1} |
| C、{x|x＞3} |
| D、{x|1≤x≤3} |
已知集合A={x|x2-6x-7＜0}，B={x|x2+2x-8≥0}，则A∪∁RB=（ ）
| A、{x|-1＜x＜7} |
| B、{x|x＞2或x＜-4 |
| C、{x|-1＜x＜2} |
| D、{x|-4＜x＜7} |
已知集合A={x∈Z|x2-1≤0}，B={x|x2-x-2=0}，则A∩B=（ ）
| A、∅ | B、{-1} |
| C、{0} | D、{2} |
函数f（x）=
+
的定义域是（ ）
| x+3 |
| (2x+3)0 | ||
|
A、[-3，
| ||||||
B、[-3，-
| ||||||
C、[-3，
| ||||||
D、[-3，-
|