题目内容
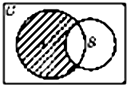 已知全集U=R,集合A={y|y=ln(x2+1),x∈R},集合A={x||x-2|≤1},则如图所示的阴影部分表示的集合为( )
已知全集U=R,集合A={y|y=ln(x2+1),x∈R},集合A={x||x-2|≤1},则如图所示的阴影部分表示的集合为( )| A、{x|0≤x<1或x>3} |
| B、{x|0≤x<1} |
| C、{x|x>3} |
| D、{x|1≤x≤3} |
考点:对数函数的定义域
专题:函数的性质及应用,集合
分析:求函数的值域化简集合A,求解绝对值的不等式化简集合B,由图得到阴影部分的集合,则求补集与交集运算得答案.
解答:
解:A={y|y=ln(x2+1),x∈R}={y|y≥0},B={x||x-2|≤1}={x|1≤x≤3},
图中阴影部分为集合A∩(∁UB),
∴∁UB={x|x<1或x>3},
∴A∩(∁UB)={x|0≤x<1或x>3}.
故选:A.
图中阴影部分为集合A∩(∁UB),
∴∁UB={x|x<1或x>3},
∴A∩(∁UB)={x|0≤x<1或x>3}.
故选:A.
点评:本题考查了函数的值域及其求法,考查了绝对值不等式的解法,考查了交集及其运算,是基础题.

练习册系列答案
相关题目
已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-2x,则当x∈[-3,0)时,f(x)的取值范围中( )
| A、[-3,0) |
| B、(0,1] |
| C、(0,3] |
| D、[-3,1] |
函数y=
的定义域为( )
log
|
A、[-
| ||||
B、(-
| ||||
| C、[-2,-1)∪(1,2] | ||||
| D、(-2,-1)∪(1,2)a>0,且a≠1y=-logaxy=ax |
已知平面向量
,
,
不共线,且两两之间的夹角都相等,若|
|=2,|
|=2,|
|=1,则
+
+
与
的夹角为( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| A、30° | B、60° |
| C、120° | D、150° |
下列说法正确的是( )
| A、某事件发生的频率是客观存在的,与试验次数无关 |
| B、某事件发生的概率为0,则该事件是不可能事件 |
| C、某事件发生的概率是随机的,在实验前不能确定 |
| D、每个实验结果出现的频率之和一定等于1 |
下列对应是集合A到集合B的映射的是( )
| A、A=N+,B=N+,f:x→|x-3| | ||
| B、A={平面内的圆},B={平面内的矩形},f:每一个圆对应它的内接矩形 | ||
C、A={0≤x≤2},B={y|0≤y≤6},f:x→y=
| ||
| D、A={0,1},B={-1,0,1},f:A中的数开平方 |