题目内容
当x∈[
,
]时,函数f(x)=cos2x+asinx的最大值为3,则a= .
| π |
| 6 |
| π |
| 2 |
考点:三角函数的最值,两角和与差的正弦函数
专题:函数的性质及应用,三角函数的求值
分析:首先把函数f(x)=cos2x+asinx通过三角恒等变换转化成以sinx为变量的二次函数的标准形式,即f(x)=-2(sinx-
)2+
+1,然后对a进行讨论①a>0②a<0其中对①a>0又分三种情况,即x=
与sinx(x∈[
,
])的关系进行单调性的探讨,通过具体的分析最后求得a值.
| a |
| 4 |
| a2 |
| 8 |
| a |
| 4 |
| π |
| 6 |
| π |
| 2 |
解答:
解:函数f(x)=cos2x+asinx=-2(sinx-
)2+
+1
所以函数f(x)是以x=
为对称轴开口方向向下的抛物线.
(1)当a<0时对称轴x=
在y轴的左侧,由于当x∈[
,
],
根据函数sinx的单调性,当x=
时,函数f(x)取得最大值,令f(
)=3 求得a=5与a<0矛盾,故舍去.
(2)当a>0时分以下三种情况进行分析:
①当
<
<1 时,即2<a<4,f(
)取得最大值为3,令f(
)=3 求得a=4 与2<a<4矛盾故舍去.
②当
≤
时,即a≤2,f(
)取得最大值3,令f(
)=3 求得a=5与a≤2矛盾故舍去.
③当
≥1时,即a≥4,f(
)取得最大值3,令 f(
)=3 求得a=4符合题意.
由(1)(2)得a=4
故答案为:4
| a |
| 4 |
| a2 |
| 8 |
所以函数f(x)是以x=
| a |
| 4 |
(1)当a<0时对称轴x=
| a |
| 4 |
| π |
| 6 |
| π |
| 2 |
根据函数sinx的单调性,当x=
| π |
| 6 |
| π |
| 6 |
(2)当a>0时分以下三种情况进行分析:
①当
| 1 |
| 2 |
| a |
| 4 |
| a |
| 4 |
| a |
| 4 |
②当
| a |
| 4 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
③当
| a |
| 4 |
| π |
| 2 |
| π |
| 2 |
由(1)(2)得a=4
故答案为:4
点评:本题考查的知识点:三角函数的变换,二次函数的标准形式,以及对称轴和sinx(x∈[
,
])的关系,重在对参数a进行分类讨论.
| π |
| 6 |
| π |
| 2 |

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
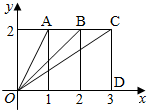 如图,三个同样大小的长方形并排一行.
如图,三个同样大小的长方形并排一行.
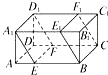 如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=4,AA1=3,分别过BC、A1D1的两个平行截面将长方体分成三部份,其体积分别记为V1=VAEA1-DFD1,V2=VEBE1A1-FCF1D1,V3=VB1E1BC1F1C,若V1:V2:V3=1:4:1,则截面A1EFD1的面积为
如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=4,AA1=3,分别过BC、A1D1的两个平行截面将长方体分成三部份,其体积分别记为V1=VAEA1-DFD1,V2=VEBE1A1-FCF1D1,V3=VB1E1BC1F1C,若V1:V2:V3=1:4:1,则截面A1EFD1的面积为