题目内容
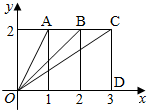如图，三个同样大小的长方形并排一行．（1）求f（x）=（
| OA |
| OC |
| OA |
| OB |
| OB |
| OC |
（2）求
| OA |
| OC |
考点：两角和与差的正切函数,数量积表示两个向量的夹角
专题：三角函数的求值,三角函数的图像与性质,平面向量及应用
分析：（1）建立平面直角坐标系，求出向量
，
，
的坐标，根据向量数量积公式，可求出
•
，
•
，
•
的值，代入可得函数解析式，结合二次函数的图象和性质，可得函数的最值；
（2）代入向量夹角公式，可得
与
夹角的余弦值，∠AOB的余弦值，进而根据同角三角函数的基本关系和两角和的正切公式，得到答案．
| OA |
| OB |
| OC |
| OA |
| OC |
| OA |
| OB |
| OB |
| OC |
（2）代入向量夹角公式，可得
| OA |
| OC |
解答：
解：（1）建立如图所示的平面直角坐标系，
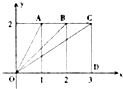
则A（1，2），B（2，2），C（3，2）
则
=（1，2），
=（2，2），
=（3，2）
•
=7，
•
=6，
•
=10，
代入f（x）=x2+6x+10，（x∈[-4，1]）
∵f（x）=x2+6x+10的图象是开口朝上，且以直线x=-3为对称轴的抛物线，
故f（x）在[-4，-3]上为减函数，在[-3，1]上为增函数，
当x=-3时，函数取最小值1，当x=1时，函数取最大值17．
（2）∵cos∠AOC=
=
=
，
cos∠AOB=
=
=
，
故sin∠AOB=
，tan∠AOB=
，
又∵tan∠COD=
，
∴tan（∠AOB+∠COD）=
=
=
则A（1，2），B（2，2），C（3，2）
则
| OA |
| OB |
| OC |
| OA |
| OC |
| OA |
| OB |
| OB |
| OC |
代入f（x）=x2+6x+10，（x∈[-4，1]）
∵f（x）=x2+6x+10的图象是开口朝上，且以直线x=-3为对称轴的抛物线，
故f（x）在[-4，-3]上为减函数，在[-3，1]上为增函数，
当x=-3时，函数取最小值1，当x=1时，函数取最大值17．
（2）∵cos∠AOC=
| ||||
|
|
| 7 | ||||
|
7
| ||
| 65 |
cos∠AOB=
| ||||
|
|
| 6 | ||||
|
3
| ||
| 10 |
故sin∠AOB=
| ||
| 10 |
| 1 |
| 3 |
又∵tan∠COD=
| 2 |
| 3 |
∴tan（∠AOB+∠COD）=
| tan∠AOB+tan∠COD |
| 1-tan∠AOB•tan∠COD |
| ||||
1-
|
| 9 |
| 7 |
点评：本题考查的知识点是两角和的正切函数，数量积表示两个向量的夹角，向量的数量积，二次函数的图象和性质，是函数，三角函数与向量的综合应用，难度中档．
练习册系列答案
每课必练系列答案
相关题目
已知|