题目内容
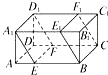 如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=4,AA1=3,分别过BC、A1D1的两个平行截面将长方体分成三部份,其体积分别记为V1=VAEA1-DFD1,V2=VEBE1A1-FCF1D1,V3=VB1E1BC1F1C,若V1:V2:V3=1:4:1,则截面A1EFD1的面积为
如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=4,AA1=3,分别过BC、A1D1的两个平行截面将长方体分成三部份,其体积分别记为V1=VAEA1-DFD1,V2=VEBE1A1-FCF1D1,V3=VB1E1BC1F1C,若V1:V2:V3=1:4:1,则截面A1EFD1的面积为考点:棱柱的结构特征
专题:空间位置关系与距离
分析:由V1:V2:V3=1:4:1,又棱柱AEA1-DFD1,EBE1A1-FCF1D1,B1E1B-C1F1C的高相等,得AE=2.由此能求出截面A1EFD1的面积.
解答:
解:V1:V2:V3=1:4:1,
又棱柱AEA1-DFD1,EBE1A1-FCF1D1,B1E1B-C1F1C的高相等,?
∴S△A1AE:SA1-EBE1:S△BB1E1=1:4:1.
∴S△A1AE=
S四边形A1ABB1=
×3×6=3,
即
×3×AE=3.解得AE=2.
在Rt△A1AE中,A1E=
=
,
∴截面A1EFD1的面积为4
.
故答案为:4
.
又棱柱AEA1-DFD1,EBE1A1-FCF1D1,B1E1B-C1F1C的高相等,?
∴S△A1AE:SA1-EBE1:S△BB1E1=1:4:1.
∴S△A1AE=
| 1 |
| 6 |
| 1 |
| 6 |
即
| 1 |
| 2 |
在Rt△A1AE中,A1E=
| 9+4 |
| 13 |
∴截面A1EFD1的面积为4
| 13 |
故答案为:4
| 13 |
点评:本题考查截面面积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
定义在R上的函数f(x)=
,若函数g(x)=lna-f(x)有4个不零点,则实数a的取值范围是( )
|
| A、(1,e)∪(e,+∞) | ||
B、(
| ||
C、(
| ||
D、(
|
已知
=(x,3),
=(3,1),且
⊥
,则x等于( )
| a |
| b |
| a |
| b |
| A、-9 | B、-1 | C、1 | D、9 |
直线2x-3y+6=0与x轴的交点是A,与y轴的交点是B,O是坐标原点则△AOB的面积是( )
| A、6 | B、3 | C、12 | D、2 |
在等比数列{an}中,a4,a12是方程x2+2011x+121=0的两根,则a8的值为( )
| A、11 | ||
| B、-11 | ||
| C、±11 | ||
D、
|