题目内容
函数y=
在区间(0,+∞)上是增函数,则实数m的取值范围是( )
| 1-3m |
| x |
A、m>
| ||
B、m≥
| ||
C、m<
| ||
D、m≤
|
考点:函数单调性的性质
专题:函数的性质及应用
分析:根据反比例函数的图象和性质,可得函数y=
在区间(0,+∞)上是增函数时,1-3m<0,进而得到答案.
| 1-3m |
| x |
解答:
解:∵函数y=
在区间(0,+∞)上是增函数,
∴1-3m<0,解得m>
,
故选:A
| 1-3m |
| x |
∴1-3m<0,解得m>
| 1 |
| 3 |
故选:A
点评:本题考查的知识点是反比例函数的单调性,熟练掌握反比例函数的图象和性质,是解答的关键.

练习册系列答案
相关题目
设y1=40.9,y2=80.5,y3=(
)-1.6,则( )
| 1 |
| 2 |
| A、y3>y1>y2 |
| B、y2>y1>y3 |
| C、y1>y2>y3 |
| D、y1>y3>y2 |
下列命题中,
①若
与
互为相反向量,则
+
=0;
②若k为实数,且k•
=
,则
=
或k=0;
③若
•
=0,则
=0或
=0;
④若
与
为平行的向量,则
•
=|
|•|
|;
⑤若|
|=1,则
=±1.
其中假命题的个数为( )
①若
| a |
| b |
| a |
| b |
②若k为实数,且k•
| a |
| 0 |
| a |
| 0 |
③若
| a |
| b |
| a |
| b |
④若
| a |
| b |
| a |
| b |
| a |
| b |
⑤若|
| a |
| a |
其中假命题的个数为( )
| A、5个 | B、4个 | C、3个 | D、2个 |
在等差数列{an}中,a3+a5=10,a7=2,则a1=( )
| A、5 | B、8 | C、10 | D、14 |
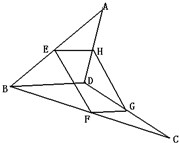 如图,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形,求证:BD∥面EFGH.
如图,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形,求证:BD∥面EFGH.