题目内容
 如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F、G分别为AC、DC、AD的中点.
如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F、G分别为AC、DC、AD的中点.(Ⅰ)求证:EF⊥平面BCG;
(Ⅱ)求三棱锥D-BCG的体积.
附:锥体的体积公式V=
| 1 |
| 3 |
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)先证明AD⊥平面BGC,利用EF∥AD,可得EF⊥平面BCG;
(Ⅱ)在平面ABC内,作AO⊥CB,交CB的延长线于O,G到平面BCD的距离h是AO长度的一半,利用VD-BCG=VG-BCD=
S△DCBh,即可求三棱锥D-BCG的体积.
(Ⅱ)在平面ABC内,作AO⊥CB,交CB的延长线于O,G到平面BCD的距离h是AO长度的一半,利用VD-BCG=VG-BCD=
| 1 |
| 3 |
解答:
 (Ⅰ)证明:∵AB=BC=BD=2.∠ABC=∠DBC=120°,
(Ⅰ)证明:∵AB=BC=BD=2.∠ABC=∠DBC=120°,
∴△ABC≌△DBC,
∴AC=DC,
∵G为AD的中点,
∴CG⊥AD.
同理BG⊥AD,
∵CG∩BG=G,
∴AD⊥平面BGC,
∵EF∥AD,
∴EF⊥平面BCG;
(Ⅱ)解:在平面ABC内,作AO⊥CB,交CB的延长线于O,
∵△ABC和△BCD所在平面互相垂直,
∴AO⊥平面BCD,
∵G为AD的中点,
∴G到平面BCD的距离h是AO长度的一半.
在△AOB中,AO=ABsin60°=
,
∴VD-BCG=VG-BCD=
S△DCBh=
•
•BD•BC•sin120°×
=
.
 (Ⅰ)证明:∵AB=BC=BD=2.∠ABC=∠DBC=120°,
(Ⅰ)证明:∵AB=BC=BD=2.∠ABC=∠DBC=120°,∴△ABC≌△DBC,
∴AC=DC,
∵G为AD的中点,
∴CG⊥AD.
同理BG⊥AD,
∵CG∩BG=G,
∴AD⊥平面BGC,
∵EF∥AD,
∴EF⊥平面BCG;
(Ⅱ)解:在平面ABC内,作AO⊥CB,交CB的延长线于O,
∵△ABC和△BCD所在平面互相垂直,
∴AO⊥平面BCD,
∵G为AD的中点,
∴G到平面BCD的距离h是AO长度的一半.
在△AOB中,AO=ABsin60°=
| 3 |
∴VD-BCG=VG-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
点评:本题考查线面垂直,考查三棱锥体积的计算,正确转换底面是关键.

练习册系列答案
相关题目
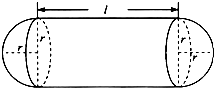 某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为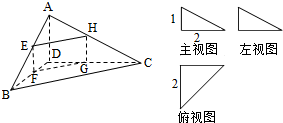 四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB、BD、DC、CA于点E、F、G、H.
四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB、BD、DC、CA于点E、F、G、H. 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,∠DAB=60°,AB=2CD=2,M是线段AB的中点.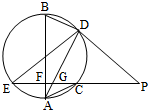 如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.