题目内容
设数列{an}的前n项的和Sn与an的关系是Sn=-an+1-
,n∈N*.
(1)求证:数列{2nan}为等差数列,并求数列{an}的通项;
(2)求数列{Sn}的前n项和Tn.
| 1 |
| 2n |
(1)求证:数列{2nan}为等差数列,并求数列{an}的通项;
(2)求数列{Sn}的前n项和Tn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由已知条件推导出2nan-2n-1an-1=
,由此能求出an=
.
(2)由(1)得Sn=1-
,从而得到Tn=n-(
+
+…+
),由此利用错位相减法能求出数列{Sn}的前n项和Tn.
| 1 |
| 2 |
| n |
| 2n+1 |
(2)由(1)得Sn=1-
| n+2 |
| 2n+1 |
| 3 |
| 22 |
| 4 |
| 23 |
| n+2 |
| 2n+1 |
解答:
解:(1)当n=1时,s1=-a1+1-
⇒a1=
…(1分),
n≥2时,由Sn-Sn-1=-an+an-1+
,
得2nan-2n-1an-1=
,
∴数列{2nan}为等差数列,…(3分)
∴2nan=2×a1+(n-1)×
,an=
.…(6分)
(2)由(1)得Sn=1-
,
∴Tn=n-(
+
+…+
),①
Tn=
n-(
+
+…+
),②
①-②得
Tn=
n-(
+
+
+…+
-
)
=
n-
-
+
=
n-1+
+
.…(9分)
∴Tn=n-2+
.…(12分)
| 1 |
| 2 |
| 1 |
| 4 |
n≥2时,由Sn-Sn-1=-an+an-1+
| 1 |
| 2n |
得2nan-2n-1an-1=
| 1 |
| 2 |
∴数列{2nan}为等差数列,…(3分)
∴2nan=2×a1+(n-1)×
| 1 |
| 2 |
| n |
| 2n+1 |
(2)由(1)得Sn=1-
| n+2 |
| 2n+1 |
∴Tn=n-(
| 3 |
| 22 |
| 4 |
| 23 |
| n+2 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 23 |
| 4 |
| 24 |
| n+2 |
| 2n+2 |
①-②得
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n+1 |
| n+2 |
| 2n+2 |
=
| 1 |
| 2 |
| 3 |
| 4 |
| ||||
1-
|
| n+2 |
| 2n+2 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 2n+4 |
| 2n+1 |
∴Tn=n-2+
| 2n+5 |
| 2n |
点评:本题考查等差数列的证明,考查数列的通项公式的证明,考查数列的前n项和的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
一个扇形的弧长与面积都是5,则这个扇形圆心角的弧度数为( )
| A、2rad | ||
B、
| ||
| C、1rad | ||
D、
|
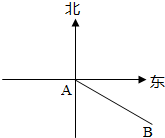 已知岛A南偏东30°方向,距岛A 20海里的B处有一缉私艇,一艘走私艇正从A处以30海里/小时的航速沿正东方向匀速行驶.假使缉私艇沿直线方向以v海里/小时的航速匀速行驶,经过t小时截住该走私船.
已知岛A南偏东30°方向,距岛A 20海里的B处有一缉私艇,一艘走私艇正从A处以30海里/小时的航速沿正东方向匀速行驶.假使缉私艇沿直线方向以v海里/小时的航速匀速行驶,经过t小时截住该走私船.