题目内容
已知函数f(x)=x2-2alnx(a∈R),
(Ⅰ)求f(x)的单调区间;
(Ⅱ)设g(x)=f(x)+2x,若g(x)在[1,2]上单调递增,求a的取值范围.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)设g(x)=f(x)+2x,若g(x)在[1,2]上单调递增,求a的取值范围.
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(I)f′(x)=2x-
=
,(x>0).对a分类讨论:当a≤0时,f′(x)>0,即可得出单调性;当a>0时,分别解出令f′(x)>0;令f′(x)<0,即可得出单调性.
(II)g(x)=f(x)+2x=x2-2alnx+2x,g′(x)=2x+2-
=
.由于g(x)在[1,2]上单调递增,g′(x)≥0在[1,2]上恒成立.转化为a≤x2+x,x∈[1,2],利用二次函数的单调性即可得出.
| 2a |
| x |
| 2x2-2a |
| x |
(II)g(x)=f(x)+2x=x2-2alnx+2x,g′(x)=2x+2-
| 2a |
| x |
| 2x2+2x-2a |
| x |
解答:
解:(I)f′(x)=2x-
=
,(x>0).
当a≤0时,f′(x)>0,函数f(x)在区间(0,+∞)上单调递增.
当a>0时,令f′(x)>0,解得x>
,函数f(x)在区间(
,+∞)上单调递增;令f′(x)<0,解得0<x<
,函数f(x)在区间(0,
)上单调递减.
综上可得:当a≤0时,函数f(x)在区间(0,+∞)上单调递增.
当a>0时,函数f(x)在区间(
,+∞)上单调递增;函数f(x)在区间(0,
)上单调递减.
(II)g(x)=f(x)+2x=x2-2alnx+2x,
g′(x)=2x+2-
=
.
由于g(x)在[1,2]上单调递增,∴g′(x)≥0在[1,2]上恒成立.
∴a≤x2+x,
∵x2+x=(x+
)2-
,在x∈[1,2]上单调递增,
∴(x2+x)min=2.
∴a≤2.
∴a的取值范围是(-∞,2].
| 2a |
| x |
| 2x2-2a |
| x |
当a≤0时,f′(x)>0,函数f(x)在区间(0,+∞)上单调递增.
当a>0时,令f′(x)>0,解得x>
| a |
| a |
| a |
| a |
综上可得:当a≤0时,函数f(x)在区间(0,+∞)上单调递增.
当a>0时,函数f(x)在区间(
| a |
| a |
(II)g(x)=f(x)+2x=x2-2alnx+2x,
g′(x)=2x+2-
| 2a |
| x |
| 2x2+2x-2a |
| x |
由于g(x)在[1,2]上单调递增,∴g′(x)≥0在[1,2]上恒成立.
∴a≤x2+x,
∵x2+x=(x+
| 1 |
| 2 |
| 1 |
| 4 |
∴(x2+x)min=2.
∴a≤2.
∴a的取值范围是(-∞,2].
点评:本题考查了利用导数研究函数的单调性极值与最值、二次函数的单调性,考查了分类讨论的思想方法,考查了恒成立问题的等价转化方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
设△ABC中,角A,B,C所对的边分别为a,b,c,则“∠C>90°”的一个充分非必要条件是( )
| A、sin2A+sin2B<sin2C | ||||||
B、sinA=
| ||||||
| C、c2>2(a+b-1) | ||||||
| D、sinA<cosB |
 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为10、高为5的等腰三角形,侧视图(或称左视图)是一个底边长为8、高为5的等腰三角形,求该几何体的表面积S.
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为10、高为5的等腰三角形,侧视图(或称左视图)是一个底边长为8、高为5的等腰三角形,求该几何体的表面积S.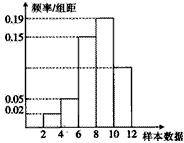 有一个容量为200的样本,其频率分布直方图如图所示,根据样本的频率分布直方图估计,样本数据落在[10,12)内的频数为
有一个容量为200的样本,其频率分布直方图如图所示,根据样本的频率分布直方图估计,样本数据落在[10,12)内的频数为