题目内容
设△ABC中,角A,B,C所对的边分别为a,b,c,则“∠C>90°”的一个充分非必要条件是( )
| A、sin2A+sin2B<sin2C | ||||||
B、sinA=
| ||||||
| C、c2>2(a+b-1) | ||||||
| D、sinA<cosB |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据充分条件和必要条件的定义,即可得到结论.
解答:
解:A.若sin2A+sin2B<sin2C,则a2+b2<c2,即∠C>90°为钝角,反之也成立.为充要条件.
B.若sinA=
,cosB=
,则cosA=
,sinB=
,
则cosC=-cos(A+B)=-[cosAcosB-sinAsinB]=-(
×
-
×
)=-
<0,则满足条件.
C.当C=90°时,如a=1,b=2,则c=
,满足c2>2(a+b-1),但此时C=90°,即充分性不成立.
D.若“∠C>90°,则“A+B<90°,即0°<A<90°-B,
∴sinA<sin(90°-B)=cosB,即为充要条件.
故选:B
B.若sinA=
| 1 |
| 4 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
则cosC=-cos(A+B)=-[cosAcosB-sinAsinB]=-(
| ||
| 4 |
| ||
| 4 |
| 1 |
| 4 |
| ||
| 4 |
| ||||
| 16 |
C.当C=90°时,如a=1,b=2,则c=
| 5 |
D.若“∠C>90°,则“A+B<90°,即0°<A<90°-B,
∴sinA<sin(90°-B)=cosB,即为充要条件.
故选:B
点评:本题主要考查充分条件和必要条件的判断,根据充分条件和必要条件的定义是解决本题的关键.

练习册系列答案
相关题目
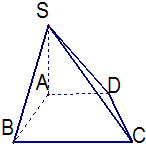 如图,四棱锥S-ABCD中,SA⊥底面ABCD,底面为等腰梯形,AD∥BC,AB=1,BC=2,AC=
如图,四棱锥S-ABCD中,SA⊥底面ABCD,底面为等腰梯形,AD∥BC,AB=1,BC=2,AC=| 3 |
| A、4π | B、5π | C、7π | D、8π |
函数f(x)=
的值域为( )
| x-4 |
| 3-x |
| A、{y|y≠-1} | ||
| B、{y|y≠4} | ||
| C、{y|y≠3} | ||
D、{y|y≠
|