题目内容
 已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为10、高为5的等腰三角形,侧视图(或称左视图)是一个底边长为8、高为5的等腰三角形,求该几何体的表面积S.
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为10、高为5的等腰三角形,侧视图(或称左视图)是一个底边长为8、高为5的等腰三角形,求该几何体的表面积S.考点:棱柱、棱锥、棱台的侧面积和表面积
专题:空间位置关系与距离
分析:根据题意,该几何体是一个四棱锥,因此利用线面垂直的性质结合勾股定理算出等腰△SAB和等腰△SCB的高长,从而算出四个侧面等腰三角形的面积,结合矩形ABCD的面积即可得到该几何体的全面积.
解答:
解:由三视图可判断几何体为四棱锥,其直观图如图:
可得该几何体是底面边长AB=10,BC=8,
且侧棱长均相等的四棱锥,高长为SO=5,如图所示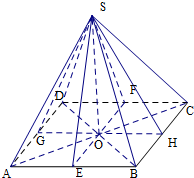
因此,SH=
=
=5
SE=
=
=
∴S△SAB=S△SCD=
×10×
=5
,
S△SCB=S△SAD=
×8×5
=20
,
∵矩形ABCD的面积为10×8=80,
∴该几何体的表面积为
S全=S△SAB+S△SCD+S△SCB+S△SAD+SABCD
=2×20
+2×5
+80=40
+10
+80.
可得该几何体是底面边长AB=10,BC=8,
且侧棱长均相等的四棱锥,高长为SO=5,如图所示

因此,SH=
| SO2+OH2 |
| 52+52 |
| 2 |
SE=
| SO2+OE2 |
| 52+42 |
| 41 |
∴S△SAB=S△SCD=
| 1 |
| 2 |
| 41 |
| 41 |
S△SCB=S△SAD=
| 1 |
| 2 |
| 2 |
| 2 |
∵矩形ABCD的面积为10×8=80,
∴该几何体的表面积为
S全=S△SAB+S△SCD+S△SCB+S△SAD+SABCD
=2×20
| 2 |
| 41 |
| 2 |
| 41 |
点评:本题主要考查空间几何体的三视图应用,根据三视图将画出立体几何的直观图是解决本题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
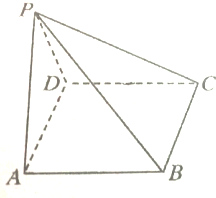 如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,且PA⊥平面ABCD,PA=5,AB=4,AD=3,求直线PC与平面ABCD所成的角.
如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,且PA⊥平面ABCD,PA=5,AB=4,AD=3,求直线PC与平面ABCD所成的角.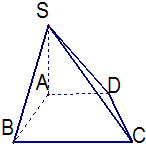 如图,四棱锥S-ABCD中,SA⊥底面ABCD,底面为等腰梯形,AD∥BC,AB=1,BC=2,AC=
如图,四棱锥S-ABCD中,SA⊥底面ABCD,底面为等腰梯形,AD∥BC,AB=1,BC=2,AC=