题目内容
过直线l：y=2x上一点P作圆C：（x-6）2+（y-2）2=5的切线l1，l2，A，B为切点，若l1，l2关于直线l对称，则∠APB= ．
考点：圆的切线方程
专题：综合题,直线与圆
分析：连接PC、AC，根据圆的性质和轴对称知识，得当切线l1，l2关于直线l对称时，直线l⊥PC，且PC平分∠APB．因此计算出圆的半径和点M到直线l的距离，在Rt△PAC中利用三角函数定义算出∠APC的度数，从而得到∠APB的度数．
解答：
解：连接PC、AC，可得当直线l1，l2关于直线l对称时，直线l⊥PC，且射线PC恰好是∠APB的平分线
∵圆C的方程为：（x-6）2+（y-2）2=5，
∴点C坐标为（6，2），半径r=
点C到直线l：2x-y=0的距离为PC=
=2
由PA切圆C于A，得Rt△PAC中，sin∠APC=
=
，得∠APC=30°
∴∠APB=2∠APC=60°
故答案为：60°
∵圆C的方程为：（x-6）2+（y-2）2=5，
∴点C坐标为（6，2），半径r=
| 5 |
点C到直线l：2x-y=0的距离为PC=
| |2×6-2| | ||
|
| 5 |
由PA切圆C于A，得Rt△PAC中，sin∠APC=
| AC |
| PC |
| 1 |
| 2 |
∴∠APB=2∠APC=60°
故答案为：60°
点评：本题在直角坐标系中给出圆的两条切线关于已知直线对称，求它们之间所成的角，着重考查了圆的标准方程、点到直线的距离、直线与圆的位置关系和轴对称等知识，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
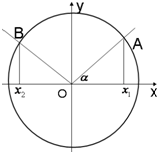已知角α的始边与x轴的非负半轴重合，终边与单位圆O交于点A（x1，y1），将射线OA按逆时针方向旋转
