题目内容
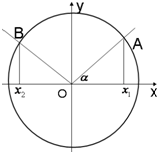已知角α的始边与x轴的非负半轴重合，终边与单位圆O交于点A（x1，y1），将射线OA按逆时针方向旋转| 2π |
| 3 |
（Ⅰ）若角α为锐角，求f（α）的取值范围；
（Ⅱ）在△ABC中，a，b，c分别是角A，B，C的对边，若f（A）=
| 3 |
| 2 |
| 3 |
考点：余弦定理,两角和与差的正弦函数
专题：三角函数的求值
分析：（Ⅰ）根据A与B为单位圆上的点，利用三角函数定义得到x1=cosα，x2=cos（α+
），进而表示出f（α），利用两角和与差的正弦、余弦函数公式化简，根据α为锐角，求出这个角的范围，利用正弦函数的值域即可确定出f（α）的取值范围；
（Ⅱ）由f（x）解析式，以及f（A）=
，利用特殊角的三角函数值求出A的度数，利用三角形面积公式列出关系式，将sinA与c的值代入求出b的值，再利用余弦定理即可求出a的值．
| 2π |
| 3 |
（Ⅱ）由f（x）解析式，以及f（A）=
| 3 |
| 2 |
解答：
解：（Ⅰ）由三角函数定义知，x1=cosα，x2=cos（α+
），
f（α）=x1-x2=cosα-cos（α+
）=
cosα+
sinα=
sin（α+
），
∵角α为锐角，
∴
＜α+
＜
，
∴
＜sin（α+
）≤1，
∴
＜
sin（α+
）≤
，
则f（α）的取值范围是（
，
]；
（Ⅱ）由f（A）=
得：sin（A+
）=
，
∵
＜A+
＜
，
∴A=
，
∵S△ABC=
bcsinA=
bc=3
，c=3，
∴b=4，
由余弦定理得：a2=b2+c2-2bccosA=16+9-12=13，
则a=
．
| 2π |
| 3 |
f（α）=x1-x2=cosα-cos（α+
| 2π |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 3 |
∵角α为锐角，
∴
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
∴
| 1 |
| 2 |
| π |
| 3 |
∴
| ||
| 2 |
| 3 |
| π |
| 3 |
| 3 |
则f（α）的取值范围是（
| ||
| 2 |
| 3 |
（Ⅱ）由f（A）=
| 3 |
| 2 |
| π |
| 3 |
| ||
| 2 |
∵
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
∴A=
| π |
| 3 |
∵S△ABC=
| 1 |
| 2 |
| ||
| 4 |
| 3 |
∴b=4，
由余弦定理得：a2=b2+c2-2bccosA=16+9-12=13，
则a=
| 13 |
点评：此题考查了余弦定理，三角形面积公式，以及两角和与差的正弦、余弦函数公式，熟练掌握公式及定理是解本题的关键．
练习册系列答案
相关题目
若对定义在R上的可导函数f（x）恒有（4-x）f（x）+xf′（x）＞0，则f（x）（ ）
| A、恒大于等于0 |
| B、恒小于0 |
| C、恒大于0 |
| D、和0的大小关系不能确定 |
如图，正四棱锥P-ABCD底面的四个顶点A，B，C，D在球O的同一个大圆上，点P在球面上，如果VP-ABCD=