题目内容
已知二次函数f(x)=ax2+bx+c(a,b,c为常数)满足条件;
①图象经过原点;②f(1-x)=f(1+x);③方程f(x)=x有等根.
(1)求f(x)的解析式
(2)若函数g(x)=|f(x)|-m有四个零点,求m的取值范围.
①图象经过原点;②f(1-x)=f(1+x);③方程f(x)=x有等根.
(1)求f(x)的解析式
(2)若函数g(x)=|f(x)|-m有四个零点,求m的取值范围.
考点:函数的零点与方程根的关系,函数解析式的求解及常用方法
专题:计算题,作图题,函数的性质及应用
分析:(1)由题意,依次确定c,a,b;从而求f(x)的解析式;
(2)函数g(x)=|f(x)|-m有四个零点可化为|f(x)|与y=m有四个不同的交点,作图求解.
(2)函数g(x)=|f(x)|-m有四个零点可化为|f(x)|与y=m有四个不同的交点,作图求解.
解答:
解:(1)由函数f(x)的图象过原点知f(0)=0,
∴c=0;
又f(1-x)=f(1+x);
∴a(1+x)2+b(1+x)=a(1-x)2+b(1-x);
整理得(2a+b)x-(2a+b)=0,
∴2a+b=0,
即a=-
;
又∵方程f(x)=x有等根,
即ax2+(b-1)x=0,
故△=0,故b=1,a=-
;
故f(x)=-
x2+x;
(2)函数g(x)=|f(x)|-m有四个零点可化为
|f(x)|与y=m有四个不同的交点,
作y=|f(x)|与y=m的图象如下,

故0<m<
.
∴c=0;
又f(1-x)=f(1+x);
∴a(1+x)2+b(1+x)=a(1-x)2+b(1-x);
整理得(2a+b)x-(2a+b)=0,
∴2a+b=0,
即a=-
| b |
| 2 |
又∵方程f(x)=x有等根,
即ax2+(b-1)x=0,
故△=0,故b=1,a=-
| 1 |
| 2 |
故f(x)=-
| 1 |
| 2 |
(2)函数g(x)=|f(x)|-m有四个零点可化为
|f(x)|与y=m有四个不同的交点,
作y=|f(x)|与y=m的图象如下,

故0<m<
| 1 |
| 2 |
点评:本题考查了二次函数的图象与性质及函数的零点与函数图象的关系应用,属于基础题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
抛物线y2=2px(p>0)的焦点为F,已知点A,B为抛物线上的两个动点,且满足∠AFB=120°.过弦AB的中点M作抛物线准线的垂线MN,垂足为N,则
的最小值为( )
| |AB| |
| |MN| |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
双曲线
-
=1上一点P到它的一个焦点的距离等于1,那么点P到另一个焦点的距离为( )
| y2 |
| 16 |
| x2 |
| 4 |
| A、5 | B、7 | C、9 | D、17 |
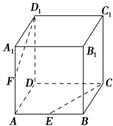 如图,在正方体ABCD-A1B1C1D1中,E、F分别是AB和AA1的中点,则下列命题:
如图,在正方体ABCD-A1B1C1D1中,E、F分别是AB和AA1的中点,则下列命题: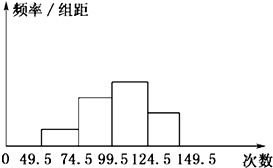 为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将取得的数据整理后,画出频率分布直方图(如图).已知图中从左到右前三个小组的频率分别为0.1,0.3,0.4,且第一小组的频数为5.
为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将取得的数据整理后,画出频率分布直方图(如图).已知图中从左到右前三个小组的频率分别为0.1,0.3,0.4,且第一小组的频数为5.