题目内容

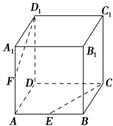如图，在正方体ABCD-A1B1C1D1中，E、F分别是AB和AA1的中点，则下列命题：
①E、C、D1、F四点共面；  ②CE、D1F、DA三线共点；③EF和BD1所成的角为90°；④A1B∥平面CD1E中，正确的是
 
．
考点：命题的真假判断与应用
专题：空间位置关系与距离,简易逻辑
分析：由三角形中位线的性质得到EF∥A1B，进一步得到EF∥D1C判断①；
由三个平面两两相交若有三条交线，交线要么相交于一点，要么互相平行判断②；
由异面直线所成角的概念判断③；由线面平行的判定定理判断④．
解答： 解：对于①，由E，F分别为AB，AA1的中点，可得EF∥A1B，又D1C∥A1B，∴EF∥D1C，则E、C、D1、F四点共面，命题①正确；
对于②，由D1FEC为平面图形，且D1F与CE相交，可得CE、D1F、DA三线共点，命题②正确；
对于③，EF和BD1所成的角等于∠A1BD1，小于90°，命题③错误；
对于④，由EF∥A1B可得A1B∥平面CD1E，命题④正确．
故答案为：①②④．
点评：本题考查了命题的真假判断与应用，考查了空间中的线面关系，训练了学生的空间想象能力和思维能力，是中档题．
练习册系列答案
相关题目
平面外两条直线在该平面上的射影互相平行，则这两条直线（　　）
A、异面B、平行
C、相交D、平行或异面
下列五个命题：
①若一个圆锥的底面半径缩小到原来的
1
2
，其体积缩小到原来的
1
4
；
②若两组数据的中位数相等，则它们的平均数也相等；
③直线x+y+1=0与圆x2+y2=
1
2
相切；
④“10a≥10b”是“lga≥lgb”的充分不必要条件．
其中真命题的序号是：
 
．
已知函数f（x）=alnx（a＞0），e为自然对数的底数．
（Ⅰ）若过点A（2，f（2））的切线斜率为2，求实数a的值；
（Ⅱ）当x＞0时，求证：f（x）≥a（1-
1
x
）；
（Ⅲ）在区间（1，e）上
f(x)
x-1
＞1恒成立，求实数a的取值范围．
已知二次函数f（x）=ax2+bx+c（a，b，c为常数）满足条件；
①图象经过原点；②f（1-x）=f（1+x）；③方程f（x）=x有等根．
（1）求f（x）的解析式
（2）若函数g（x）=|f（x）|-m有四个零点，求m的取值范围．
已知函数f（x）满足f（x+y）=f（x）+f（y），当x＞0时，有f（x）＜0，且f（1）=-2
（1）求f（0）及f（-1）的值；
（2）判断函数f（x）的单调性，并加以证明；
（3）求解不等式f（2x）-f（x2+3x）＜4．
已知函数f（x）=sinx+acosx的图象经过点（
π
3
，0）
（1）求实数a的值；
（2）设g（x）=[f（x）]2-2，求当x∈（
π
4
，
2π
3
）时，函数g（x）的值域；
（3）若g（
a
2
）=-
3
4
（
π
6
＜a＜
2π
3
），求cos（α+
3π
2
）的值．
函数f（x）=2sin（2x-
π
3
）+3的最小值为（　　）
A、5B、1C、3D、4
函数f（x）=
1
2
sin2x-
3
2
cos2x+1的单调递增区间为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网