Question

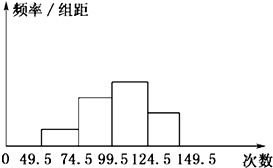为了了解小学生的体能情况，抽取了某校一个年级的部分学生进行一分钟跳绳次数测试，将取得的数据整理后，画出频率分布直方图（如图）．已知图中从左到右前三个小组的频率分别为0.1，0.3，0.4，且第一小组的频数为5．
（1）求第四小组的频率；
（2）参加这次测试的学生一共有多少人？
（3）若次数在75次以上（含75次）为达标，试估计该年级学生在跳绳测试中的达标率是多少？

Answer 1

考点：频率分布直方图

专题：概率与统计

分析：（1）由频率累加和为1，求出第四小组的频率；
（2）根据频率、频数与样本容量的关系，求出参加这次测试的学生数；
（3）求出次数在75次以上（含75次）的频率即可．

解答： 解：（1）由频率累加和为1知，第四小组的频率为
1-0.1-0.3-0.4=0.2；
（2）设参加这次测试的学生有x人，
则0.1x=5，解得=50，
即参加这次测试的学生有50人；
（3）次数在75次以上（含75次）的频率为
0.3+0.4+0.2=0.9，
∴达标率为90%．

点评：本题考查了频率分布直方图的应用问题，解题时应根据分布直方图进行有关的计算，是基础题目．