题目内容
已知函数f(x)=x2eax.
(Ⅰ)当a=1时,求f(x)在(1,f(1))处的切线方程;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)若f(x)在(1,+∞)单调递增,求a的取值范围.
(Ⅰ)当a=1时,求f(x)在(1,f(1))处的切线方程;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)若f(x)在(1,+∞)单调递增,求a的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)当a=1时,求导函数,确定切线的斜率,求出切点的坐标,即可求f(x)在(1,f(1))处的切线方程;
(Ⅱ)分类讨论,利用导数的正负,可求函数f(x)的单调区间;
(Ⅲ)利用(Ⅱ)的结论,结合f(x)在(1,+∞)单调递增,即可求a范围.
(Ⅱ)分类讨论,利用导数的正负,可求函数f(x)的单调区间;
(Ⅲ)利用(Ⅱ)的结论,结合f(x)在(1,+∞)单调递增,即可求a范围.
解答:
解:(Ⅰ)当 a=1时,f(x)=x2ex,f′(x)=(x2)′ex+x2(ex)′=2xex+x2ex=(2x+x2)ex
∴f′(1)=3e,f(1)=e,
∴切线方程为y-e=3e(x-1),即3ex-y-2e=0…(4分)
(Ⅱ)f′(x)=(x2)′eax+x2(eax)′=2xeax+ax2eax=x(ax+2)eax…(5分)
(1)当a=0时,f′(x)=2x,当x>0时,f′(x)>0,当x<0时,f′(x)<0,
∴单调增区间为(0,+∞),单调减区间为(-∞,0)…(6分)
当a≠0时,令f′(x)=0,得x1=0或x2=-
…(7分)
(2)当a>0时,0>-
,
当x<-
时,f′(x)>0,当-
<x<0时,f′(x)<0,当x>0时,f′(x)>0,
单调增区间为(-∞,-
),(0,+∞),单调减区间为(-
,0)…(9分)
(3)当a<0时,0<-
,当x>-
时,f′(x)<0,当0<x<-
时,f′(x)>0,当x<0时,f′(x)<0,
∴f(x)的单调增区间是(0,-
),单调减区间是(-∞,0),(-
,+∞) …(11分)
综上:当a=0时,单调增区间为(0,+∞),单调减区间为(-∞,0)
当a>0时,单调增区间为(-∞,-
),(0,+∞),单调减区间为(-
,0)
当a<0时,f(x)的单调增区间是(0,-
),单调减区间是(-∞,0),(-
,+∞)
(Ⅲ)由(Ⅱ)知,当a≥0时,f(x)在(0,+∞)单调递增,满足条件; …(12分)
当a<0时,单调增区间为(0,-
)与f(x)在(1,+∞)单调递增不符 …(13分)
综上:a≥0 …(14分)
∴f′(1)=3e,f(1)=e,
∴切线方程为y-e=3e(x-1),即3ex-y-2e=0…(4分)
(Ⅱ)f′(x)=(x2)′eax+x2(eax)′=2xeax+ax2eax=x(ax+2)eax…(5分)
(1)当a=0时,f′(x)=2x,当x>0时,f′(x)>0,当x<0时,f′(x)<0,
∴单调增区间为(0,+∞),单调减区间为(-∞,0)…(6分)
当a≠0时,令f′(x)=0,得x1=0或x2=-
| 2 |
| a |
(2)当a>0时,0>-
| 2 |
| a |
当x<-
| 2 |
| a |
| 2 |
| a |
单调增区间为(-∞,-
| 2 |
| a |
| 2 |
| a |
(3)当a<0时,0<-
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
∴f(x)的单调增区间是(0,-
| 2 |
| a |
| 2 |
| a |
综上:当a=0时,单调增区间为(0,+∞),单调减区间为(-∞,0)
当a>0时,单调增区间为(-∞,-
| 2 |
| a |
| 2 |
| a |
当a<0时,f(x)的单调增区间是(0,-
| 2 |
| a |
| 2 |
| a |
(Ⅲ)由(Ⅱ)知,当a≥0时,f(x)在(0,+∞)单调递增,满足条件; …(12分)
当a<0时,单调增区间为(0,-
| 2 |
| a |
综上:a≥0 …(14分)
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查分类讨论的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
在球O内任取一点P,则P点在球O的内接正四面体中的概率是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
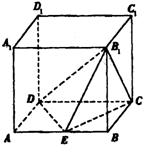 如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点.设正方体的棱长为2a.
如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点.设正方体的棱长为2a. 已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1).
已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1).