题目内容
已知圆C的方程为x2+y2-4x=0,直线l与x,y轴的交点坐标分别为(
,0)和(0,-
),则直线l截圆C所得的弦长为 .
| 1 |
| 3 |
| 1 |
| 4 |
考点:直线与圆的位置关系
专题:直线与圆
分析:利用截距式求得直线l的方程,求出圆心(2,0)到直线l的距离d和圆的半径r,再由弦长公式求得直线l截圆C所得的弦长.
解答:
解:由直线l与x,y轴的交点坐标分别为(
,0)和(0,-
),
可得直线l的方程为
+
=1,即 3x-4y-1=0.
圆心(2,0)到直线l的距离d=
=1,圆C:x2+y2-4x=0的半径等于2,
故直线l截圆C所得的弦长为 2
=2
=2
,
故答案为 2
.
| 1 |
| 3 |
| 1 |
| 4 |
可得直线l的方程为
| x | ||
|
| y | ||
-
|
圆心(2,0)到直线l的距离d=
| |6-0-1| | ||
|
故直线l截圆C所得的弦长为 2
| r2-d2 |
| 4-1 |
| 3 |
故答案为 2
| 3 |
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
函数f(x)=3cos
-log
x零点个数是( )
| πx |
| 2 |
| 1 |
| 2 |
| A、2 | B、3 | C、4 | D、5 |
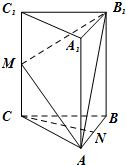 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,