题目内容
 已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1).
已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1).(Ⅰ)求抛物线的标准方程;
(Ⅱ)是否存在直线l:y=kx+t,与圆x2+(y+1)2=1相切且与抛物线交于不同的两点M,N,当∠MON为钝角时,有S△MON=48成立?若存在,求出直线的方程,若不存在,说明理由.
考点:直线与圆的位置关系,平面向量数量积的运算,抛物线的标准方程
专题:压轴题,圆锥曲线的定义、性质与方程
分析:(Ⅰ) 设抛物线方程为x2=2py,把点(2,1)代入运算求得 p的值,即可求得抛物线的标准方程.
(Ⅱ) 由直线与圆相切可得
=1⇒k2=t2+2t.把直线方程代入抛物线方程并整理,由△>0求得t的范围.利用根与系数的关系及
•
<0,求得|MN| =4
,求得点O到直线的距离,从而求得S△MON=2
,由此函数在(0,4)单调递增,故有0<S△MON<16
,从而得出结论.
(Ⅱ) 由直线与圆相切可得
| |t+1| | ||
|
| OM |
| ON |
| (1+k2)(t2+3t) |
| t4+3t3 |
| 7 |
解答:
解:(Ⅰ) 设抛物线方程为x2=2py,
由已知得:22=2p,所以 p=2,
所以抛物线的标准方程为 x2=4y.
(Ⅱ) 不存在.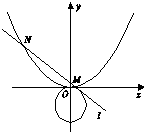
因为直线与圆相切,所以
=1⇒k2=t2+2t.
把直线方程代入抛物线方程并整理得:x2-4kx-4t=0.
由△=16k2+16t=16(t2+2t)+16t>0,得 t>0或t<-3.
设M(x1,y1),N(x2,y2),则x1+x2=4k且x1•x2=-4t,
∴y1•y2=(kx1+t)•(kx2+t)=k2x1x2+kt(x1+x2)+t2=t2.
∵∠MON为钝角,∴
•
<0,解得0<t<4,∵|MN|=
|x1-x2|=4
,
点O到直线的距离为
,∴S△MON=2
,易证f(t)=2
在(0,4)单调递增,
∴0<S△MON<16
,故不存在直线,当∠MON为钝角时,S△MON=48成立.
由已知得:22=2p,所以 p=2,
所以抛物线的标准方程为 x2=4y.
(Ⅱ) 不存在.

因为直线与圆相切,所以
| |t+1| | ||
|
把直线方程代入抛物线方程并整理得:x2-4kx-4t=0.
由△=16k2+16t=16(t2+2t)+16t>0,得 t>0或t<-3.
设M(x1,y1),N(x2,y2),则x1+x2=4k且x1•x2=-4t,
∴y1•y2=(kx1+t)•(kx2+t)=k2x1x2+kt(x1+x2)+t2=t2.
∵∠MON为钝角,∴
| OM |
| ON |
| 1+k2 |
| (1+k2)(t2+3t) |
点O到直线的距离为
| |t| | ||
|
| t4+3t3 |
| t4+3t3 |
∴0<S△MON<16
| 7 |
点评:本题主要考查直线和圆的位置关系,两个向量的数量积公式的应用,点到直线的距离公式,利用函数的单调性求函数的值域,属于中档题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2.若对任意的x∈[a,a+2],不等式f(x+a)≥f(
x)恒成立,则实数a的取值范围是( )
| 2 |
| A、a≤0 | ||
B、a≥
| ||
C、a≤
| ||
| D、a≥0 |
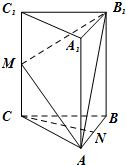 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,