题目内容
设k∈R,若1≤x≤2时恒有x3-3x2+2≤(1-k)x+1≤0,则k的取值集合是 .
考点:函数恒成立问题
专题:综合题,不等式的解法及应用
分析:1≤x≤2时恒有(1-k)x+1≤0,可得kk≥2;x3-3x2+2≤(1-k)x+1,则1-k≥x2-3x+
,求出1≤x≤2时,右边的最大值,可求k的取值集合.
| 1 |
| x |
解答:
解:∵1≤x≤2时恒有(1-k)x+1≤0,
∴
,
∴k≥2.
x3-3x2+2≤(1-k)x+1,则1-k≥x2-3x+
,
令f(x)=x2-3x+
,则
设f′(x)=2x-3-
=0在1≤x≤2时的解为a,
∴函数在(1,a)上单调减,在(a,2)上单调增,
∵f(1)=-1,f(2)=-
,
∴f(x)max=f(1)=-1,
∴1-k≥-1,
∴k≤2.
∴k的取值集合是{2}.
故答案为:{2}.
∴
|
∴k≥2.
x3-3x2+2≤(1-k)x+1,则1-k≥x2-3x+
| 1 |
| x |
令f(x)=x2-3x+
| 1 |
| x |
设f′(x)=2x-3-
| 1 |
| x2 |
∴函数在(1,a)上单调减,在(a,2)上单调增,
∵f(1)=-1,f(2)=-
| 3 |
| 2 |
∴f(x)max=f(1)=-1,
∴1-k≥-1,
∴k≤2.
∴k的取值集合是{2}.
故答案为:{2}.
点评:本题考查函数恒成立问题,考查导数知识的运用,确定函数的最大值是关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
将函数y=cos2x的图象向右平移
个单位,得到y=cos(2x+φ),φ∈(-π,π]的图象,则φ的值为( )
| π |
| 6 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
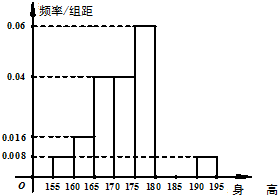 从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.