题目内容
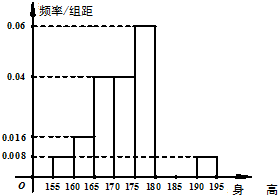 从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.(Ⅰ)求第七组的频率并估计该校800名男生中身高在180cm以上(含180cm)的人数;
(Ⅱ)从第六组和第八组的男生中随机抽取两名男生,记他们的身高分别为x,y,事件E={|x-y|≤5},求P(E).
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:(Ⅰ)先由第六组的人数除以样本容量得到第六组的频率,然后用1减去出第七组外各组的频率和即可得到第七组的频率;因为过中位数的直线两侧的矩形的面积相等,经计算前三组的频率和小于0.5,后四组的频率和大于0.5,由此断定中位数位于第四组,设出中位数m,由0.04+0.08+0.2+(m-170)×0.04=0.5即可求得中位数m的值;
(II)分别求出第六组和第八组的人数,利用列举法列出从身高属于第六组和第八组的所有男生中随机抽取两名男生的总的方法,再根据古典概型的概率公式解之即可.
(II)分别求出第六组和第八组的人数,利用列举法列出从身高属于第六组和第八组的所有男生中随机抽取两名男生的总的方法,再根据古典概型的概率公式解之即可.
解答:
解:(Ⅰ)第六组的频率为
=0.08,
所以第七组的频率为1-0.08-5×(0.008×2+0.016+0.04×2+0.06)=0.06;
由直方图得后三组频率为0.06+0.08+0.008×5=0.18,
所以800名男生中身高在180cm以上(含180cm)的人数为0.18×800=144人-----------(6分)
(Ⅱ)第六组[180,185)的人数为4人,设为a,b,c,d,
第八组[190,195]的人数为2人,设为A,B,
则从中抽取两人有ab,ac,ad,bc,bd,cd,aA,bA,cA,dA,aB,bB,cB,dB,AB共15种情况,
因事件E={|x-y|≤5}发生当且仅当随机抽取的两名男生在同一组,
所以事件E包含的基本事件为ab,ac,ad,bc,bd,cd,AB共7种情况,
故P(E)=
.-----------(12分)
| 4 |
| 50 |
所以第七组的频率为1-0.08-5×(0.008×2+0.016+0.04×2+0.06)=0.06;
由直方图得后三组频率为0.06+0.08+0.008×5=0.18,
所以800名男生中身高在180cm以上(含180cm)的人数为0.18×800=144人-----------(6分)
(Ⅱ)第六组[180,185)的人数为4人,设为a,b,c,d,
第八组[190,195]的人数为2人,设为A,B,
则从中抽取两人有ab,ac,ad,bc,bd,cd,aA,bA,cA,dA,aB,bB,cB,dB,AB共15种情况,
因事件E={|x-y|≤5}发生当且仅当随机抽取的两名男生在同一组,
所以事件E包含的基本事件为ab,ac,ad,bc,bd,cd,AB共7种情况,
故P(E)=
| 7 |
| 15 |
点评:本题考查了频率分布直方图,考查了列举法求基本事件及事件发生的概率,解答此题的关键是明确频率直方图中各矩形的频率和等于1,中位数是频率分布直方图中,过该点的直线把各矩形面积均分的点的横坐标,此题是基础题.

练习册系列答案
相关题目
如图所示,程序框图(算法流程图)的输出值s=( )


| A、-1 | B、0 | C、1 | D、3 |
已知i为虚数单位,若
是纯虚数,则实数a的值为( )
| a+i |
| 1-i |
A、-
| ||
| B、-1 | ||
| C、1 | ||
D、
|
“x>3”是“x2>9”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、既充分又必要条件 |
| D、既不充分又不必要条件 |
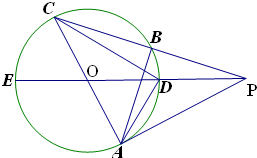 如图,PA是⊙O的切线,PE过圆心0,AC为⊙O的直径,PC与⊙O相交于B、C两点,连接AB、CD.
如图,PA是⊙O的切线,PE过圆心0,AC为⊙O的直径,PC与⊙O相交于B、C两点,连接AB、CD. 在线路中,各原件能否正常工作是相互独立的,已知原件a,b,c,d,e能正常工作的概率是0.9,0.95,0.7,0.8,0.85,求线路畅通的概率.
在线路中,各原件能否正常工作是相互独立的,已知原件a,b,c,d,e能正常工作的概率是0.9,0.95,0.7,0.8,0.85,求线路畅通的概率.