题目内容
过点(2-
,0)(n∈N*)且方向向量为(2,1)的直线交椭圆
+y2=1于An,Bn两点,记原点为O,△OAnBn面积为Sn,则
Sn= .
| 1 |
| n |
| x2 |
| 4 |
| lim |
| n→∞ |
考点:椭圆的简单性质,极限及其运算
专题:圆锥曲线的定义、性质与方程
分析:由题意可得直线的方程,与椭圆的方程联立可得根与系数的关系,利用弦长公式可得|AnBn|,再利用点到直线的距离公式可得原点O到直线AnBn的距离dn.利用三角形的面积计算公式可得Sn=
dn|AnBn|.再利用极限的运算法则即可得出.
| 1 |
| 2 |
解答:
解:如图所示,
过点(2-
,0)(n∈N*)且方向向量为(2,1)的直线ln的方程为:y=
(x-2+
).
联立
,化为2x2+2(
-2)x+
-
=0.
∴x1+x2=2-
,x1x2=
(
-
).
∴|AnBn|=
=
=
.
原点O到直线AnBn的距离dn=
=
.
∴Sn=
dn|AnBn|=
×
×
.
∴
Sn=
×
×
=1.
故答案为:1.

过点(2-
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| n |
联立
|
| 1 |
| n |
| 1 |
| n2 |
| 4 |
| n |
∴x1+x2=2-
| 1 |
| n |
| 1 |
| 2 |
| 1 |
| n2 |
| 4 |
| n |
∴|AnBn|=
(1+
|
|
|
原点O到直线AnBn的距离dn=
|0-1+
| ||||
|
2-
| ||
|
∴Sn=
| 1 |
| 2 |
| 1 |
| 2 |
2-
| ||
|
|
∴
| lim |
| n→∞ |
| 1 |
| 2 |
| 2-0 | ||
|
|
故答案为:1.
点评:本题考查了直线的方向向量与斜率的关系、直线与椭圆相交问题转化为方程联立得到根与系数的关系、弦长公式、点到直线的距离公式、三角形的面积计算公式、极限的运算法则等基础知识与基本技能方法,考查了计算能力和推理能力,属于难题.

练习册系列答案
相关题目
下列各式中值等于
的是( )
| 1 |
| 2 |
| A、sin15°cos15° | ||||||
B、
| ||||||
C、cos2
| ||||||
D、
|
方程1-z4=0在复数范围内的根共有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
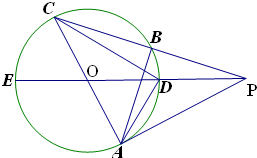 如图,PA是⊙O的切线,PE过圆心0,AC为⊙O的直径,PC与⊙O相交于B、C两点,连接AB、CD.
如图,PA是⊙O的切线,PE过圆心0,AC为⊙O的直径,PC与⊙O相交于B、C两点,连接AB、CD.