题目内容
2.已知点A是以BC为直径的圆O上异于B,C的动点,P为平面ABC外一点,且平面PBC⊥平面ABC,BC=3,PB=2$\sqrt{2}$,PC=$\sqrt{5}$,则三棱锥P-ABC外接球的表面积为10π.分析 由O为△ABC外接圆的圆心,且平面PBC⊥平面ABC,过O作面ABC的垂线l,则垂线l一定在面PBC内,可得球心O1一定在面PBC内,即球心O1也是△PBC外接圆的圆心,
在△PBC中,由余弦定理、正弦定理可得R即可,
解答  解:因为O为△ABC外接圆的圆心,且平面PBC⊥平面ABC,过O作面ABC的垂线l,则垂线l一定在面PBC内,
解:因为O为△ABC外接圆的圆心,且平面PBC⊥平面ABC,过O作面ABC的垂线l,则垂线l一定在面PBC内,
根据球的性质,球心一定在垂线l,
∵球心O1一定在面PBC内,即球心O1也是△PBC外接圆的圆心,
在△PBC中,由余弦定理得cosB=$\frac{P{B}^{2}+B{C}^{2}-P{C}^{2}}{2BP•BC}=\frac{\sqrt{2}}{2}$,⇒sinB=$\frac{\sqrt{2}}{2}$,
由正弦定理得:$\frac{PC}{sinB}=2R$,解得R=$\frac{\sqrt{10}}{2}$,
∴三棱锥P-ABC外接球的表面积为s=4πR2=10π,
故答案为:10π.
点评 本题考查了三棱锥的外接球的表面积,将空间问题转化为平面问题,利用正余弦定理是解题的关键,属于中档题.

练习册系列答案
相关题目
12.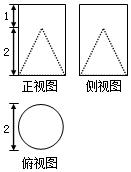 在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示,则此工艺部件的表面积为( )
在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示,则此工艺部件的表面积为( )
 在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示,则此工艺部件的表面积为( )
在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示,则此工艺部件的表面积为( )| A. | (7+$\sqrt{5}$)π | B. | (7+2$\sqrt{5}$)π | C. | (8+$\sqrt{5}$)π | D. | (8+2$\sqrt{5}$)π |
13.若(ax+2)4展开式中含有x3项的系数为8则$\int_a^{e^2}{\frac{1}{x}dx=}$( )
| A. | .2 | B. | .$-\frac{1}{e^2}-1$ | C. | .$-\frac{1}{e^2}+1$ | D. | 2-e |
17.把曲线的极坐标方程ρ=8sinθ化为直角坐标方程式( )
| A. | x2+y2=4 | B. | x2+(y-4)2=16 | C. | x2+y2=1 | D. | y=2x2 |
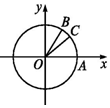 在如图所示的直角坐标系xOy中,点A,B是单位圆上的点,且A(1,0),∠AOB=$\frac{π}{3}$.现有一动点C在单位圆的劣弧$\widehat{AB}$上运动,设∠AOC=α.
在如图所示的直角坐标系xOy中,点A,B是单位圆上的点,且A(1,0),∠AOB=$\frac{π}{3}$.现有一动点C在单位圆的劣弧$\widehat{AB}$上运动,设∠AOC=α.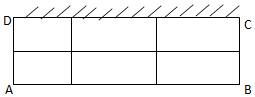 某养猪厂建造一间背面靠墙的长方形猪圈,已知猪圈地面面积为18平方米,将猪圈分割成(如图所示)六个小猪圈,猪圈高度为1米,猪圈每平方米的造价为500元,且不计猪圈背面和地面的费用与猪圈的厚度,问怎样设计总造价最低,最低造价是多少?
某养猪厂建造一间背面靠墙的长方形猪圈,已知猪圈地面面积为18平方米,将猪圈分割成(如图所示)六个小猪圈,猪圈高度为1米,猪圈每平方米的造价为500元,且不计猪圈背面和地面的费用与猪圈的厚度,问怎样设计总造价最低,最低造价是多少?