题目内容
12．
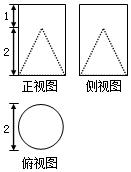在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示，则此工艺部件的表面积为（ ）| A． | （7+$\sqrt{5}$）π | B． | （7+2$\sqrt{5}$）π | C． | （8+$\sqrt{5}$）π | D． | （8+2$\sqrt{5}$）π |
分析 通过三视图可知该几何体中圆柱高、底面半径以及圆锥的高，进而利用公式分别计算出圆柱侧面积、圆柱上底面面积、圆锥侧面积，相加即得结论．
解答 
解：由三视图可知，该几何体中圆柱高h=3，底面半径R=1，圆锥的高h'=2，
圆柱侧面积S1=2πRh=6π，
圆柱上底面面积S2=πR2=π，
圆锥侧面积S3=πR$\sqrt{{R}^{2}+（h'）^{2}}$=$\sqrt{5}$π，
则所求表面积为S1+S2+S3=6π+π+$\sqrt{5}$π=7π+$\sqrt{5}$π，
故选：A．
点评 本题考查通过三视图求几何体的表面积，涉及圆锥、圆柱的侧面积，注意解题方法的积累，属于中档题．
练习册系列答案
相关题目
3．若a＞0，b＞0，且42a+b=2ab，则a+b的最小值是（ ）
| A． | 12 | B． | 6+2$\sqrt{2}$ | C． | 6+4$\sqrt{2}$ | D． | 6+4$\sqrt{3}$ |
20．若关于x的不等式x2+ax-c＜0的解集为{x|-2＜x＜1}，且函数$y=a{x^3}+m{x^2}+x+\frac{c}{2}$在区间$（{\frac{1}{2}，1}）$上不是单调函数，则实数m的取值范围是（ ）
| A． | $（-2，-\sqrt{3}）$ | B． | $[{-3，-\sqrt{3}}]$ | C． | $（{-∞，-2}）∪（{\sqrt{3}，+∞}）$ | D． | $（{-∞，-2}）∪（{-\sqrt{3}，+∞}）$ |