题目内容
用辗转相除法求8251与6105的最大公约数．
考点：辗转相除法
专题：算法和程序框图
分析：用较大的数字除以较小的数字，得到商和余数，然后再用上一式中的除数和得到的余数中较大的除以较小的，以此类推，当整除时，就得到要求的最大公约数．
解答：
解：8251=6105×1+2146
6105=2146×2+1813
2146=1813×1+333
333=148×2+37
148=37×4
所以8251与6105的最大公约数就是37．
6105=2146×2+1813
2146=1813×1+333
333=148×2+37
148=37×4
所以8251与6105的最大公约数就是37．
点评：本题考查用辗转相除法求两个数的最大公约数，本题是一个基础题，在解题时注意数字的运算不要出错，注意与更相减损术进行比较．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
把正整数按如图所示的规律排列，则从2003到2005的箭头方向依次为（ ）
| A、↓ 2004→ |
| B、↑ →2004 |
| C、2004→ ↑ |
| D、→2004 ↓ |
在复平面内，复数z=sin3+icos3对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
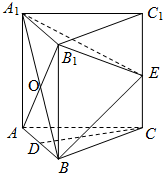如图，在三棱柱ABC-A1B1C1中，每个侧面均为正方形，D为底边AB的中点，E为侧棱CC1的中点．