题目内容
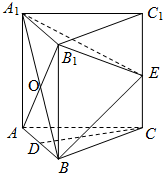 如图,在三棱柱ABC-A1B1C1中,每个侧面均为正方形,D为底边AB的中点,E为侧棱CC1的中点.
如图,在三棱柱ABC-A1B1C1中,每个侧面均为正方形,D为底边AB的中点,E为侧棱CC1的中点.(1)求证:CD∥平面A1EB;
(2)求证:CD⊥平面A1ABB1.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(1)设AB1和A1B的交点为O,连接EO,连接OD,根据三角形中位线定理可以证明四边形ECOD为平行四边形,再利用直线与平面平行的判定定理进行证明,即可解决问题;
(2)利用线面垂直的判定定理,即可证明.
(2)利用线面垂直的判定定理,即可证明.
解答:
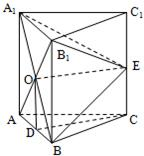 证明:(1)设AB1和A1B的交点为O,连接EO,连接OD.
证明:(1)设AB1和A1B的交点为O,连接EO,连接OD.
因为O为AB1的中点,D为AB的中点,
所以OD∥BB1且OD=
BB1.
又E是CC1中点,
所以EC∥BB1且EC=
BB1,
所以EC∥OD且EC=OD.
所以,四边形ECOD为平行四边形.所以EO∥CD.
又CD?平面A1BE,EO?平面A1BE,则CD∥平面A1BE;
(2)因为在三棱柱ABC-A1B1C1中,每个侧面均为正方形,D为底边AB的中点,
所以CD⊥AB,CD⊥A1A,
因为A1A∩AB=A,
所以CD⊥平面A1ABB1.
 证明:(1)设AB1和A1B的交点为O,连接EO,连接OD.
证明:(1)设AB1和A1B的交点为O,连接EO,连接OD.因为O为AB1的中点,D为AB的中点,
所以OD∥BB1且OD=
| 1 |
| 2 |
又E是CC1中点,
所以EC∥BB1且EC=
| 1 |
| 2 |
所以EC∥OD且EC=OD.
所以,四边形ECOD为平行四边形.所以EO∥CD.
又CD?平面A1BE,EO?平面A1BE,则CD∥平面A1BE;
(2)因为在三棱柱ABC-A1B1C1中,每个侧面均为正方形,D为底边AB的中点,
所以CD⊥AB,CD⊥A1A,
因为A1A∩AB=A,
所以CD⊥平面A1ABB1.
点评:本题考查直线与平面平行,直线与平面垂直的判断与证明,考查空间想象能力,逻辑推理能力.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
已知
=(l+2,0,2l),
=(6,2m-1,2),若
∥
,则l与m的值分别为( )
| a |
| b |
| a |
| b |
A、
| ||||
| B、5,2 | ||||
C、-
| ||||
| D、-5,-2 |
函数f(x)=2sin
x与g(x)=
图象所有交点的横坐标之和为( )
| π |
| 2 |
| 3 | x-2 |
| A、12 | B、14 | C、16 | D、18 |
已知正项等比数列数列{an},bn=logaan,则数列{bn}是 ( )
| A、等比数列 |
| B、等差数列 |
| C、既是等差数列又是等比数列 |
| D、以上都不对 |