题目内容
设点A(1,-1),B(0,1),C(1,1),直线l:ax+by=1,已知直线l与线段AB(不含B点)无公共点,且直线l与包含端点的线段AC有公共点,则z=2a+b的最小值为( )
| A、5 | B、4 | C、2 | D、1 |
考点:简单线性规划,直线的斜率
专题:数形结合,转化思想,直线与圆
分析:由题意列出a,b所满足的约束条件,画出可行域,数形结合得到最优解,求出最优解的坐标,代入目标函数得答案.
解答:
解:如图,
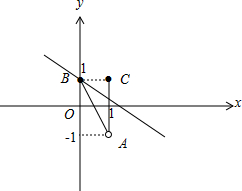
将直线改l:ax+by=1写为ax+by-1=0,
直线l与线段AB(不含B点)无公共点,且直线l与包含端点的线段AC有公共点,
得
,
画出可行域如图,

化z=2a+b为b=-2a+z,
由图可知,当直线b=-2a+z过(0,1)时直线在b轴上的截距最小,为z=2×0+1=1.
故选:D.

将直线改l:ax+by=1写为ax+by-1=0,
直线l与线段AB(不含B点)无公共点,且直线l与包含端点的线段AC有公共点,
得
|
画出可行域如图,

化z=2a+b为b=-2a+z,
由图可知,当直线b=-2a+z过(0,1)时直线在b轴上的截距最小,为z=2×0+1=1.
故选:D.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,考查了数学转化思想方法,是中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
已知函数y=ax的反函数是f(x)且f(
)=
,则a=( )
| 2 |
| 1 |
| 2 |
| A、4 | ||
B、
| ||
C、
| ||
| D、2 |
设α为锐角,若cos(α+
)=
,则sin(2α+
)的值为( )
| π |
| 6 |
| 4 |
| 5 |
| π |
| 12 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知a=log34,b=log43,c=log53,则a,b,c的大小关系是( )
| A、c<a<b |
| B、b<a<c |
| C、a<c<b |
| D、c<b<a |
已知等差数列{an}中,a1007=4,S2014=2014,则S2015=( )
| A、-2015 | B、2015 |
| C、-4030 | D、4030 |
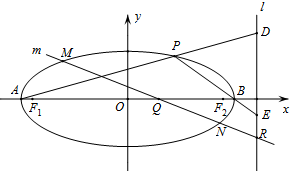 椭圆C的方程为
椭圆C的方程为 某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示.
某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示.