题目内容
 某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示.
某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示.(Ⅰ)分别求第3,4,5组的频率;
(Ⅱ)该校决定在第3,4,5组中用分层抽样抽取6名学生进行问卷调查,然后再从这6名学生中随机抽取2名学生进行面谈,若这2名学生中有ξ名学生是第4组的,求ξ的分布列和数学期望.
考点:离散型随机变量及其分布列,离散型随机变量的期望与方差
专题:概率与统计
分析:(Ⅰ)直接利用频率分布直方图求解第3,4,5组的频率;
(Ⅱ)该校决定在第3,4,5组中用分层抽样抽取6名学生进行问卷调查,然后再从这6名学生中随机抽取2名学生进行面谈,若这2名学生中有ξ名学生是第4组的,得到随机变量的概率,列出ξ的分布列,然后求解数学期望.
(Ⅱ)该校决定在第3,4,5组中用分层抽样抽取6名学生进行问卷调查,然后再从这6名学生中随机抽取2名学生进行面谈,若这2名学生中有ξ名学生是第4组的,得到随机变量的概率,列出ξ的分布列,然后求解数学期望.
解答:
解:(Ⅰ)第3组的频率为0.06×5=0.3;
第4组的频率为0.04×5=0.2;
第5组的频率为0.02×5=0.1;
(Ⅱ)由题知,第3,4,5组抽取的学生数学分别为3,2,1,
∴ξ取0,1,2.
因为P(ξ=0)=
=
,P(ξ=1)=
=
,P(ξ=2)=
=
,
所以,ξ的分布列为:
∴Eξ=0×
+1×
+2×
=
.
第4组的频率为0.04×5=0.2;
第5组的频率为0.02×5=0.1;
(Ⅱ)由题知,第3,4,5组抽取的学生数学分别为3,2,1,
∴ξ取0,1,2.
因为P(ξ=0)=
| ||||
|
| 2 |
| 5 |
| ||||
|
| 8 |
| 15 |
| ||||
|
| 1 |
| 15 |
所以,ξ的分布列为:
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 2 |
| 5 |
| 8 |
| 15 |
| 1 |
| 15 |
| 2 |
| 3 |
点评:本题考查频率分布直方图、概率、分层抽样、随机变量的分布列与期望等基础知识,考查学生应用知识解决问题的能力,中等题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=log3
的图象( )
| 1+x |
| 1-x |
| A、关于原点对称 |
| B、关于直线y=-x对称 |
| C、关于y轴对称 |
| D、关于直线y=x对称 |
设点A(1,-1),B(0,1),C(1,1),直线l:ax+by=1,已知直线l与线段AB(不含B点)无公共点,且直线l与包含端点的线段AC有公共点,则z=2a+b的最小值为( )
| A、5 | B、4 | C、2 | D、1 |
已知a>b>0,则下列命题正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知命题p:?x∈R,x2≥0,则( )
| A、¬p:?x∈R,x2≥0 |
| B、¬p:?x∈R,x2<0 |
| C、¬p:?x∈R,x2≤0 |
| D、¬p:?x∈R,x2<0 |
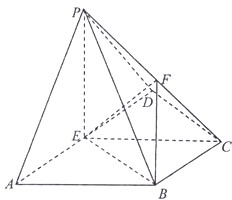 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD是梯形,BC∥AD,E,F分别是AD,PC的中点,△ABE,△BEC,△ECD都是边长为1的等边三角形.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD是梯形,BC∥AD,E,F分别是AD,PC的中点,△ABE,△BEC,△ECD都是边长为1的等边三角形.