题目内容
已知等差数列{an}中，a1007=4，S2014=2014，则S2015=（ ）
| A、-2015 | B、2015 |
| C、-4030 | D、4030 |
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：由等差数列的求和公式和性质可得a1008=-2，再由求和公式和性质可得S2015=2015a1008=-4030
解答：
解：由题意可得S2014=
=1007（a1007+a1008）=2014，
∴a1007+a1008=2，
又∵a1007=4，∴a1008=-2，
∴S2015=
=
=2015a1008=-4030
故选：C
| 2014(a1+a2014) |
| 2 |
∴a1007+a1008=2，
又∵a1007=4，∴a1008=-2，
∴S2015=
| 2015(a1+a2015) |
| 2 |
| 2015×2a1008 |
| 2 |
故选：C
点评：本题考查等差数列的求和公式和性质，属基础题．
练习册系列答案
相关题目
设点A（1，-1），B（0，1），C（1，1），直线l：ax+by=1，已知直线l与线段AB（不含B点）无公共点，且直线l与包含端点的线段AC有公共点，则z=2a+b的最小值为（ ）
| A、5 | B、4 | C、2 | D、1 |
已知命题p：?x∈R，x2≥0，则（ ）
| A、￢p：?x∈R，x2≥0 |
| B、￢p：?x∈R，x2＜0 |
| C、￢p：?x∈R，x2≤0 |
| D、￢p：?x∈R，x2＜0 |
下列函数中，与函数y=x有相同图象的一个函数是（ ）
A、y=
| ||
B、y=
| ||
| C、y=logaax | ||
D、y=（
|
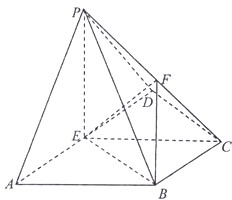如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，ABCD是梯形，BC∥AD，E，F分别是AD，PC的中点，△ABE，△BEC，△ECD都是边长为1的等边三角形．