题目内容
 椭圆C的方程为
椭圆C的方程为| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
(Ⅰ)求椭圆C的方程;
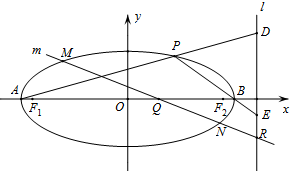
(Ⅱ)设椭圆的左、右顶点分别为A、B,直线l的方程为x=4,P是椭圆上异于A、B的任意一点,直线PA、PB分别交直线l于D、E两点,求
| F1D |
| F2E |
(Ⅲ)过点Q(1,0)任意作直线m(与x轴不垂直)与椭圆C交于M、N两点,与l交于R点,
| RM |
| MQ |
| RN |
| NQ |
考点:直线与圆锥曲线的综合问题,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用已知条件求出b,a,然后求椭圆C的方程;
(Ⅱ)设P(x0,y0),推出直线PA、PB的方程,求得D,E两点的坐标求出向量,利用点P(x0,y0)在椭圆C上,即可求
•
的值;
(Ⅲ)设M(x1,y1),N(x2,y2),R(4,t),利用
=x
,得到:
(λ≠-1),代入椭圆方程,化简,由
=y
得(4+y)2+9t2=9(1+y)2,然后消去t,即可得到4x+4y+5=0.
(Ⅱ)设P(x0,y0),推出直线PA、PB的方程,求得D,E两点的坐标求出向量,利用点P(x0,y0)在椭圆C上,即可求
| F1D |
| F2E |
(Ⅲ)设M(x1,y1),N(x2,y2),R(4,t),利用
| RM |
| MQ |
|
| RN |
| NQ |
解答:
解:(Ⅰ)椭圆C的方程为
+
=1(a>b>0),F1、F2分别是它的左、右焦点,已知椭圆C过点(0,1),且离心率e=
,所以b=1,
=
,解得a=3,
所求椭圆方程为:
+y2=1…4分
(Ⅱ)设P(x0,y0),则直线PA、PB的方程分别为y=
(x+3),y=
(x-3),
将x=4分别代入可求得D,E两点的坐标分别为D(4,
),E(4,
).
由(Ⅰ),F1(-2
,0),F2(2
,0),
所以
•
=(4+2
,
)•(4-2
,
)=8+
,
又∵点P(x0,y0)在椭圆C上,
∴
+
=1⇒
=-
,
∴
•
=
.…8分
(Ⅲ)证明:设M(x1,y1),N(x2,y2),R(4,t),
由
=x
得(x1-4,y1-t)=x(1-x1,-y1)
所以
(λ≠-1),代入椭圆方程得 (4+x)2+9t2=9(1+x)2①
同理由
=y
得(4+y)2+9t2=9(1+y)2②
①-②消去t,得x+y=-
,所以4x+4y+5=0.…13分.
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
| a2-b2 |
| a2 |
| 8 |
| 9 |
所求椭圆方程为:
| x2 |
| 9 |
(Ⅱ)设P(x0,y0),则直线PA、PB的方程分别为y=
| y0 |
| x0+3 |
| y0 |
| x0-3 |
将x=4分别代入可求得D,E两点的坐标分别为D(4,
| 7y0 |
| x0+3 |
| y0 |
| x0-3 |
由(Ⅰ),F1(-2
| 2 |
| 2 |
所以
| F1D |
| F2E |
| 2 |
| 7y0 |
| x0+3 |
| 2 |
| y0 |
| x0-3 |
7
| ||
|
又∵点P(x0,y0)在椭圆C上,
∴
| ||
| 9 |
| y | 2 0 |
| ||
|
| 1 |
| 9 |
∴
| F1D |
| F2E |
| 65 |
| 9 |
(Ⅲ)证明:设M(x1,y1),N(x2,y2),R(4,t),
由
| RM |
| MQ |
所以
|
同理由
| RN |
| NQ |
①-②消去t,得x+y=-
| 5 |
| 4 |
点评:本题考查椭圆的相关知识,直线与椭圆的位置关系的应用,考查学生运算能力、分析问题的能力,较难题.

练习册系列答案
相关题目
已知直线y=-x+m是曲线y=x2-3lnx的一条切线,则m的值为( )
| A、0 | B、2 | C、1 | D、3 |
定义域为R的可导函数y=f(x)的导函数为f′(x),满足f(x)>f′(x)且f(0)=1,则不等式
<1的解为( )
| f(x) |
| ex |
| A、(-∞,0) |
| B、(0,+∞) |
| C、(-∞,2) |
| D、(2,+∞) |
函数y=log3
的图象( )
| 1+x |
| 1-x |
| A、关于原点对称 |
| B、关于直线y=-x对称 |
| C、关于y轴对称 |
| D、关于直线y=x对称 |
设点A(1,-1),B(0,1),C(1,1),直线l:ax+by=1,已知直线l与线段AB(不含B点)无公共点,且直线l与包含端点的线段AC有公共点,则z=2a+b的最小值为( )
| A、5 | B、4 | C、2 | D、1 |
已知a>b>0,则下列命题正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
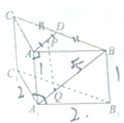 如图,三棱柱ABC-A1B1C1,侧棱AA1⊥平面ABC,A1B1=A1C1=2,AA1=1,∠B1A1C1=120°,D是BC的中点,P是AD的中点,点Q在A1B上且BQ=3QA1
如图,三棱柱ABC-A1B1C1,侧棱AA1⊥平面ABC,A1B1=A1C1=2,AA1=1,∠B1A1C1=120°,D是BC的中点,P是AD的中点,点Q在A1B上且BQ=3QA1