题目内容
已知
与
的夹角为
，且
•
=
，则|
-
|的最小值为（ ）
| a |
| b |
| π |
| 6 |
| a |
| b |
| 3 |
| a |
| b |
A、4-2
| ||
B、
| ||
C、
| ||
D、4+2
|
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由题意可得|
|•|
|=2，根据|
-
|=
=
，利用基本不等式求得它的最小值．
| a |
| b |
| a |
| b |
(
|
|
解答：
解：由题意可得
•
=|
|•|
|•cos
=
，∴|
|•|
|=2．
∵|
-
|=
=
≥
=
=
-1，
当且仅当|
|=|
|时取等号，故|
-
|的最小值为
-1，
故选：C．
| a |
| b |
| a |
| b |
| π |
| 6 |
| 3 |
| a |
| b |
∵|
| a |
| b |
(
|
|
2|
|
4-2
|
| 3 |
当且仅当|
| a |
| b |
| a |
| b |
| 3 |
故选：C．
点评：本题主要考查两个向量的数量积的定义、基本不等式，求向量的模，属于中档题．
练习册系列答案
相关题目
已知数列{an}对任意的m、n∈N*，满足am+n=am+an，且a2=1，那么a10等于（ ）
| A、3 | B、5 | C、7 | D、9 |
已知斜三棱柱的三视图如图，该斜三棱柱的体积为（ ）
| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
公差不为零的等差数列{an}的前n项和为Sn，若a3是a2与a6的等比中项，S4=8，则S6=（ ）
| A、18 | B、24 | C、60 | D、90 |
己知命题“?x∈R，使x2+（a+1）x+1≤0”是假命题，则实数a的取值范围是（ ）
| A、（-∞，-3）∪（1，+∞） |
| B、（-∞，-3]∪[1，+∞） |
| C、（-3，1） |
| D、[-3，1] |
某几何体的三视图如图所示，则它的体积是（ ）
| A、5 | ||
| B、6 | ||
C、
| ||
D、
|
设全集U=R，M={x|x2+3x＜0}，N={x|y=
}，则图中阴影部分表示的集合为（ ）
| -x-1 |
| A、{x|x＞-1} |
| B、{x|-3＜x＜0} |
| C、{x|x≤-3} |
| D、{x|-1＜x＜0} |
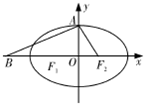如图，设椭圆C：