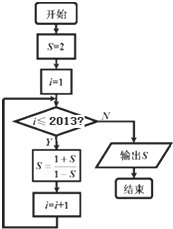
��Ŀ����
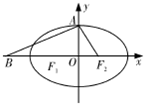 ��ͼ������ԲC��
��ͼ������ԲC��| x2 |
| a2 |
| y2 |
| b2 |
| BF1 |
| F1F2 |
| AB |
| AF2 |
��1������A��B��F2�����Բǡ����ֱ��l1��x-
| 3 |
��2���ڣ�1���������£����ҽ���F2��б��Ϊk��ֱ��l����ԲC����M��N���㣬��x�����Ƿ���ڵ�P��m��0��ʹ����PM��PNΪ�ڱߵ�ƽ���ı��������Σ�������ڣ����m��ȡֵ��Χ����������ڣ�˵�����ɣ�
���㣺ֱ����Բ���ߵ��ۺ�����
ר�⣺Բ�����е���ֵ�뷶Χ����
��������1����B��x0��0��������֪�����Ƶ���x0=-
��b2=3c2���Ӷ��õ�a=2c������
=2c���������ԲC�ķ��̣�
��2���ɣ�1��֪F2��1��0����l��y=k��x-1��������
���ã�3+4k2��x2-8k2x+4k2-12=0���ɴ�����Τ�ﶨ�������֪���������������������ĵ�P����m��ȡֵ��Χ�ǣ�0��
����
| b2 |
| c |
| |-c-3| |
| 2 |
��2���ɣ�1��֪F2��1��0����l��y=k��x-1��������
|
| 1 |
| 4 |
���
�⣺��1����B��x0��0������F2��c��0����A��0��b����
��
=(x0��-b)��
=(c��-b)��
��
•
=0����cx0+b2=0����x0=-
��
��
=
����F1ΪBF2�е㣬
��-
+c=-2c��b2=3c2��
�Ӷ�a2=4c2����a=2c��
��
•
=0����
��
��
���ABF2�����Բ��Բ��ΪF1��-c��0�����뾶r=
|F2B|=2c��
��ֱ��l2 ��x-
y-3=0���ABF2�����Բ���У�
��
=2c�����c=1����a=2��b=
��
����ԲC�ķ���Ϊ
+
=1��
��2���ɣ�1��֪F2��1��0����l��y=k��x-1����
����
���ã�3+4k2��x2-8k2x+4k2-12=0��
��M��x1��y1����N��x2��y2������x1+x2=
��
y1+y2=k��x1+x2-2����
+
=��x1-m��y1��+��x2-m��y2��=��x1+x2-2m��y1+y2����
�����εĶԽ����ഹֱ���ࣨ
+
��•
=0��
�ࣨx1+x2-2m��y1+y2��•��x2-x1��y2-y1��=0��
�ࣨx1+x2-2m����x2-x1��+��y1+y2����y2-y1��=0��
��y2 -y1=k(x2-x1)��0��
�ࣨx1+x2-2m��+k��y1+y2��=0��
��
-2m+k2(
-2)=0��
������֪k��R��k��0��
��m=
=
��
��0��m��
��
�������������ĵ�P����m��ȡֵ��Χ�ǣ�0��
����
��
| AB |
| AF2 |
��
| AB |
| AF2 |
| b2 |
| c |
��
| BF1 |
| F1F2 |
��-
| b2 |
| c |
�Ӷ�a2=4c2����a=2c��
��
| AB |
| AF2 |
| AB |
| AF2 |
���ABF2�����Բ��Բ��ΪF1��-c��0�����뾶r=
| 1 |
| 2 |
��ֱ��l2 ��x-
| 3 |
��
| |-c-3| |
| 2 |
| 3 |
����ԲC�ķ���Ϊ
| x2 |
| 4 |
| y2 |
| 3 |
��2���ɣ�1��֪F2��1��0����l��y=k��x-1����
����
|
��M��x1��y1����N��x2��y2������x1+x2=
| 8k2 |
| 3+4k2 |
y1+y2=k��x1+x2-2����
| PM |
| PN |
�����εĶԽ����ഹֱ���ࣨ
| PM |
| PN |
| MN |
�ࣨx1+x2-2m��y1+y2��•��x2-x1��y2-y1��=0��
�ࣨx1+x2-2m����x2-x1��+��y1+y2����y2-y1��=0��
��y2 -y1=k(x2-x1)��0��
�ࣨx1+x2-2m��+k��y1+y2��=0��
��
| 8k2 |
| 3+4k2 |
| 8k2 |
| 3+4k2 |
������֪k��R��k��0��
��m=
| k2 |
| 3+4k2 |
| 1 | ||
|
��0��m��
| 1 |
| 4 |
�������������ĵ�P����m��ȡֵ��Χ�ǣ�0��
| 1 |
| 4 |
���������⿼����Բ���̵����������������ĵ�������Ƿ���ڵ��ж���������ʱҪ�������⣬ע��ȼ�ת��˼��ͺ����뷽��˼��ĺ������ã�

��ϰ��ϵ�д�
�����Ŀ
��֪
��
�ļн�Ϊ
����
•
=
����|
-
|����СֵΪ��������
| a |
| b |
| �� |
| 6 |
| a |
| b |
| 3 |
| a |
| b |
A��4-2
| ||
B��
| ||
C��
| ||
D��4+2
|
��ƽ��ֱ������ϵxOy�У�ԲC�ķ���Ϊx2+y2-4x=0����ֱ��y=k��x+1���ϴ���һ��P��ʹ��P������Բ�������������ֱ����ʵ��k��ȡֵ��Χ�ǣ�������
A����-�ޣ�-2
| ||||||||
B��[-2
| ||||||||
C��[-
| ||||||||
D����-�ޣ�-2
|
ij�����ͼ��ͼ��ʾ�������������ĸ����������������ĺ����ǣ�������
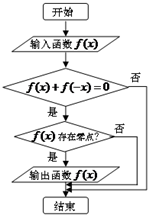

| A��f��x��=lnx | ||
B��f��x��=
| ||
| C��f��x��=ex | ||
| D��f��x��=x3 |