题目内容
已知斜三棱柱的三视图如图,该斜三棱柱的体积为( )


| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:判断斜三棱柱的底面三角形的形状,棱柱的高,即可求解三棱柱的体积.
解答:
解:由三视图知:斜三棱柱的底面是直角边长为1和2的直接三角形,棱柱的高为:2.
写三棱柱的体积为:V=
×1×2×2=2.
故选:A.

写三棱柱的体积为:V=
| 1 |
| 2 |
故选:A.

点评:本题考查三视图求解几何体的体积,判断几何体的形状是解题的关键.

练习册系列答案
相关题目
 将半径为2的圆分成相等的四弧,再将四弧围成星形放在半径为2的圆内,现在往该圆内任投一点,此点落在星形内的概率为( )
将半径为2的圆分成相等的四弧,再将四弧围成星形放在半径为2的圆内,现在往该圆内任投一点,此点落在星形内的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
复数z=
-
的虚部为( )
| 1+i |
| i |
| i |
| 1+i |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
执行如图所示程序框图,则输出的S的值为( )


| A、21 | B、25 | C、45 | D、93 |
设x,y满足
,则z=x-y( )
|
| A、有最小值2,无最大值 |
| B、有最小值-1,无最大值 |
| C、有最大值2,无最小值 |
| D、既无最小值,又无最大值 |
已知
与
的夹角为
,且
•
=
,则|
-
|的最小值为( )
| a |
| b |
| π |
| 6 |
| a |
| b |
| 3 |
| a |
| b |
A、4-2
| ||
B、
| ||
C、
| ||
D、4+2
|
在△ABC中,AC=
,AB=3,BC=2,M,N,P分别为AC,AB,BC中点,将△ABC沿MN,NP,MP折起得到三棱锥S-MNP,三棱锥S-MNP外接球的表面积为( )
| 7 |
| A、10π | ||
| B、8π | ||
| C、5π | ||
D、
|
某程序框图如图所示,现输入如下四个函数,则可以输出的函数是( )
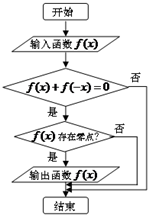

| A、f(x)=lnx | ||
B、f(x)=
| ||
| C、f(x)=ex | ||
| D、f(x)=x3 |
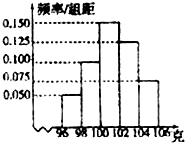 某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分散直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于102克的产品的个数是
某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分散直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于102克的产品的个数是