题目内容
已知函数①f(x)=x2;②f(x)=ex;③f(x)=lnx;④f(x)=cosx.其中对于f(x)定义域内的任意一个x1都存在唯一的x2,使f(x1)f(x2)=1成立的函数是 .
考点:函数的图象
专题:函数的性质及应用
分析:对于函数①③④,可以采用反例法进行否定,对于函数②,可以直接推导命题成立.
解答:
解:对于函数①,取x1=2,则有x2=-
或
与之对应,不惟一,故①不符题意;
对于函数③取x1=1,此时f(x1)=0,则不存在x2,使f(x1)f(x2)=1,故③不符题意;
对于函数④取x1=0,则当x2=2kπ,k∈Z时,有无数多个x2,使得使f(x1)f(x2)=1成立,故④不符题意;
对于函数②,定义域为R,任取x1,有ex1>0恒成立,取x2使得ex1•ex2=1,则ex1+x2=1,
所以x1+x2=0,所以x2=-x1∈R,且唯一.
故答案为:②.
| ||
| 2 |
| ||
| 2 |
对于函数③取x1=1,此时f(x1)=0,则不存在x2,使f(x1)f(x2)=1,故③不符题意;
对于函数④取x1=0,则当x2=2kπ,k∈Z时,有无数多个x2,使得使f(x1)f(x2)=1成立,故④不符题意;
对于函数②,定义域为R,任取x1,有ex1>0恒成立,取x2使得ex1•ex2=1,则ex1+x2=1,
所以x1+x2=0,所以x2=-x1∈R,且唯一.
故答案为:②.
点评:在选择或填空题中,对于一些全称命题的真假判断,往往采用反例法进行否定.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
在等差数列{an}中,已知a2与a4是方程x2-6x+8=0的两个根,若a4>a2,则a2014=( )
| A、2012 | B、2013 |
| C、2014 | D、2015 |
 将半径为2的圆分成相等的四弧,再将四弧围成星形放在半径为2的圆内,现在往该圆内任投一点,此点落在星形内的概率为( )
将半径为2的圆分成相等的四弧,再将四弧围成星形放在半径为2的圆内,现在往该圆内任投一点,此点落在星形内的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知
与
的夹角为
,且
•
=
,则|
-
|的最小值为( )
| a |
| b |
| π |
| 6 |
| a |
| b |
| 3 |
| a |
| b |
A、4-2
| ||
B、
| ||
C、
| ||
D、4+2
|
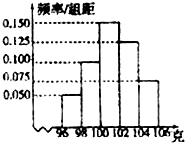 某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分散直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于102克的产品的个数是
某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分散直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于102克的产品的个数是