题目内容
设全集U=R，M={x|x2+3x＜0}，N={x|y=
}，则图中阴影部分表示的集合为（ ）
| -x-1 |
| A、{x|x＞-1} |
| B、{x|-3＜x＜0} |
| C、{x|x≤-3} |
| D、{x|-1＜x＜0} |
考点：Venn图表达集合的关系及运算
专题：集合
分析：由题意分别求不等式x2+3x＜0的解集和函数y=
的定义域，从而求出集合M、N；再根据图形阴影部分表示的集合是CUN∩M，得到答案．
| -x-1 |
解答：
解：∵M={x|x2+3x＜0}={x|-3＜x＜0}，
N={x|y=
}={x|x≤-1}，
则图中阴影部分表示的集合是CUN∩M={x|-3＜x＜0}∩{x|x＞-1}={x|-1＜x＜0}，
故选D．
N={x|y=
| -x-1 |
则图中阴影部分表示的集合是CUN∩M={x|-3＜x＜0}∩{x|x＞-1}={x|-1＜x＜0}，
故选D．
点评：本题考查了求Venn图表示得集合，关键是根据图形会判断出阴影部分表示的集合元素特征，再通过集合运算求出．
练习册系列答案
全能测控一本好卷系列答案
相关题目
将半径为2的圆分成相等的四弧，再将四弧围成星形放在半径为2的圆内，现在往该圆内任投一点，此点落在星形内的概率为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知
与
的夹角为
，且
•
=
，则|
-
|的最小值为（ ）
| a |
| b |
| π |
| 6 |
| a |
| b |
| 3 |
| a |
| b |
A、4-2
| ||
B、
| ||
C、
| ||
D、4+2
|
在△ABC中，AC=
，AB=3，BC=2，M，N，P分别为AC，AB，BC中点，将△ABC沿MN，NP，MP折起得到三棱锥S-MNP，三棱锥S-MNP外接球的表面积为（ ）
| 7 |
| A、10π | ||
| B、8π | ||
| C、5π | ||
D、
|
执行如图所示的程序框图，若输出的结果为21，则判断框中应填（ ）
| A、i＜5 | B、i＜6 |
| C、i＜7 | D、i＜8 |
在平面直角坐标系xOy中，圆C的方程为x2+y2-4x=0．若直线y=k（x+1）上存在一点P，使过P所作的圆的两条切线相互垂直，则实数k的取值范围是（ ）
A、（-∞，-2
| ||||||||
B、[-2
| ||||||||
C、[-
| ||||||||
D、（-∞，-2
|
某程序框图如图所示，现输入如下四个函数，则可以输出的函数是（ ）
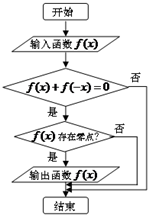
| A、f（x）=lnx | ||
B、f（x）=
| ||
| C、f（x）=ex | ||
| D、f（x）=x3 |